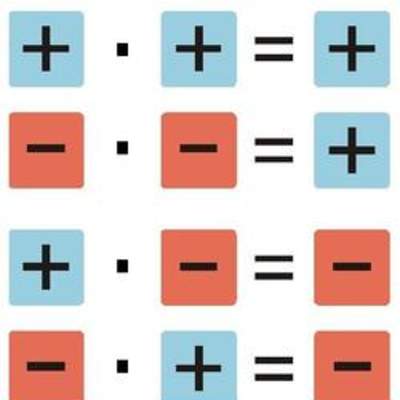Priorización 2023-2025: Aprendizajes Basales
MA08 OA 01
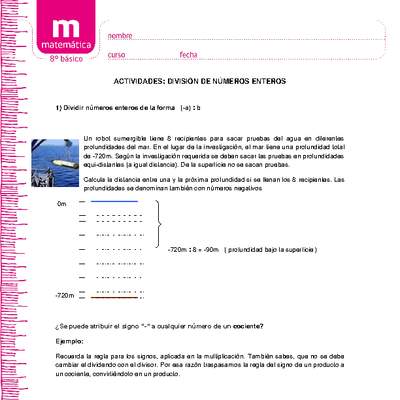
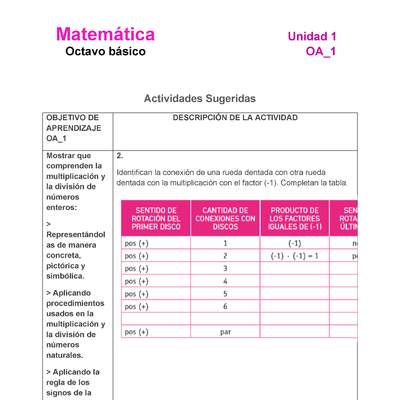
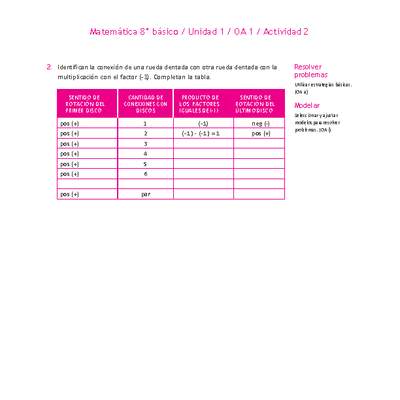
Mostrar que comprenden la multiplicación y la división de números enteros:
- Representándolos de manera concreta, pictórica y simbólica.
- Aplicando procedimientos usados en la multiplicación y la división de números naturales.
- Aplicando la regla de los signos de la operación.
- Resolviendo problemas rutinarios y no rutinarios.
Textos Escolares oficiales 2023
Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 1
Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico
Material didáctico
Evaluaciones del programa
Unidad 0Unidad 1
Indicadores
Indicadores Unidad 1
- Representan la multiplicación por -1 de manera concreta; por ejemplo: con situaciones o procesos inversos (estar en contra de, etc.).
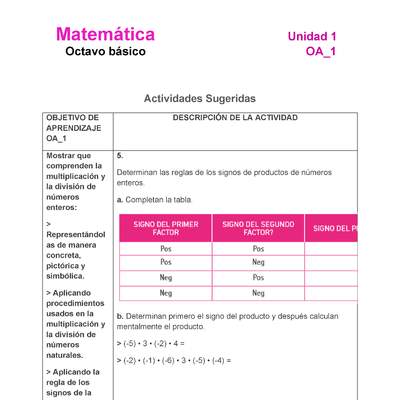
- Desarrollan la regla de los signos en ejemplos concretos o en la recta numérica: + • + = +; + • - = -; - • + = -; - • - = +.
- Representan la multiplicación de números enteros positivos y negativos de forma pictórica (recta numérica) o simbólica.
- Aplican la regla de los signos de las multiplicaciones y de las divisiones en ejercicios rutinarios.
- Representan, de forma concreta o pictórica, la división de un número negativo por un número natural.
- Multiplican números enteros positivos y/o negativos, utilizando la multiplicación de números naturales y la regla de los signos.
- Resuelven problemas cotidianos que requieren la multiplicación o división de números enteros.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Regla de los signos
Enunciado
¿Cuál es el resultado de la siguiente expresión?
$(-1)\cdot (-1)\cdot (-1)\cdot (-1)+ (-1)\cdot (-1)\cdot (-1) -(-1)=$
Alternativas
A) $(-1)$
B) $1$
C) $(-2)$
D) $2$
Regla de los signos
Enunciado
¿Cuál es el resultado de la siguiente expresión?
$(-1)\cdot (-2)\cdot 3-(1\cdot 2\cdot (-3))+((-1)\cdot (-2)\cdot3)=$
Alternativas
A) $18$
B) $(-18)$
C) $6$
D) $-6$
Regla de los signos con enteros
Enunciado
¿Cuál es el resultado del siguiente ejercicio?
$-5\cdot(-3)\cdot(-1)\cdot (2) \cdot (-1)=$
Alternativas
A) $30$
B) $-30$
C) $60$
D) $-60$
Regla de los signos con enteros
Enunciado
¿Qué número divide a $-30$ para obtener $-2$?
Alternativas
A) $-2$
B) $2$
C) $15$
D) $-15$
Estación espacial MIR
Enunciado
La estación espacial Mir permaneció en órbita durante 15 años y giró alrededor de la Tierra unas 86 500 veces durante su permanencia en el espacio.
La estadía más prolongada de un cosmonauta en la Mir fue de aproximadamente 680 días.
¿Aproximadamente, cuántas veces giró este cosmonauta alrededor de la Tierra?
Alternativas
A) 110
B) 1 100
C) 11 000
D) 110 000
Bicicletas
Enunciado
Pedro, Cecilia y Julio usan bicicletas de distinto tamaño. En la siguiente tabla se muestra la distancia que avanzan sus bicicletas por cada giro completo de las ruedas.
| Distancia viajada en cm | ||||||
| 1 vuelta | 2 vueltas | 3 vueltas | 4 vueltas | 5 vueltas | 6 vueltas | |
| Pedro | 96 | 192 | 288 | 384 | 480 | $\cdots$ |
| Cecilia | 160 | 320 | 480 | 640 | 800 | $\cdots$ |
| Julio | 190 | 380 | 570 | 760 | 950 | $\cdots$ |
¿Cuántas vueltas tiene que dar la rueda de la bicicleta de Cecilia para avanzar 1280 cm?
Respuesta : ________ vueltas.
Skateboard
Enunciado
Eric es un fanático del skateboard. Visita una tienda para comprobar algunos precios.
En la tienda se puede comprar un skate completo. También se puede comprar por separado una tabla, un juego de $4$ ruedas, un juego de dos ejes y un juego de accesorios, y armar el skate uno mismo.
Los precios para los productos de la tienda son:
| Producto | Precio en zeds |
| Skate completo | $82$ u $84$ |
| Tabla | $40$, $60$ ó $65$ |
| Un juego de $4$ ruedas | $14$ ó $36$ |
| Un juego de $2$ ejes | $16$ |
| Un juego de accesorios (rodamientos cuñas de goma pernos y tuercas) |
$10$ ó $20$ |
Eric quiere armar su propio skate. ¿Cuál es el precio mínimo y el precio máximo en esta tienda para un skate armado por uno mismo?
(a) Precio mínimo: ________ zeds.
(b) Precio máximo: ________ zeds.
Banco de Preguntas [Banco de preguntas-MA8 OA01-1313] Matemática 8
Enunciado
Si $\textbf{n}$ y $\textbf{m}$ son enteros negativos, ¿cuál de las siguientes expresiones también es negativa?
I. $mn$
II. $\dfrac{m}{n}$
III. $m+n$
Alternativas
A) Solo III.
B) Solo I y II.
C) Solo I y III.
D) I, II y III.
Banco de Preguntas [Banco de preguntas-MA8 OA01-3825] Matemática 8
Enunciado
Un avión debe descender $400$ metros en $5$ minutos. Si el avión desciende de manera constante; es decir, nunca aumenta o disminuye la velocidad, ¿cuál es la velocidad a la que desciende por cada minuto que pasa?
Alternativas
A) $80$ $m$
B) $-80$ $m$
C) $-800$ $m$
D) $800$ $m$
Multiplicación y división de números enteros
Enunciado
Si $b=-2$ entonces $\dfrac{32}{b-6}+\dfrac{40}{b-8}=$
Alternativas
A) $-1$
B) $-2$
C) $8$
D) $-8$
¿Cuál es el valor de esta expresión?
Enunciado
Si x = -3, ¿cuál es el valor de -3x?
Alternativas
A) -9
B) -1
C) 1
D) 9
¿Cuál es el valor de este producto de números enteros?
Enunciado
¿Cuál es el valor de la siguiente expresión?
1 - 5 • (-2)
Alternativas
A) 11
B) 8
C) -8
D) -9
Número entero impar
Enunciado
¿Cuál de las siguientes opciones es siempre un número entero impar?
Alternativas
A) La suma de tres números enteros pares.
B) La suma de dos números enteros impares.
C) El producto de dos números enteros impares.
D) El producto de tres números enteros consecutivos.
Número mayor
Enunciado
Si n es un número entero negativo, ¿cuál de estos números es el mayor?
Alternativas
A) 3 : n
B) 3 - n
C) 3 . n
D) 3 + n
Representación de enteros con profundidades
Enunciado
Una especie marina comienza su vida a 150 metros de profundidad en las costas australes de Chile.
Si se sabe que cada mes desciende 7 metros, ¿cuál será su profundidad después de un año de vida?
Alternativas
A) $150 + 12·(-7) = 66$ metros.
B) $150 + 12·7 = 234$ metros.
C) $-150 + 12·7 = -66$ metros.
D) $-150 + 12·(-7) = -234$ metros.
