Priorización 2023-2025: Aprendizajes Basales
MA1M OA 03
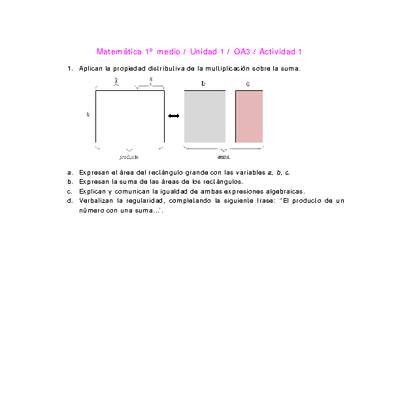
Desarrollar los productos notables de manera concreta, pictórica y simbólica:
- Transformando productos en sumas y viceversa.
- Aplicándolos a situaciones concretas.
- Completando el cuadrado del binomio.
- Utilizándolas en la reducción y desarrollo de expresiones algebraicas.
Textos Escolares oficiales 2023
Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 1
Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico
Material didáctico
Lecciones: clases completas
Evaluaciones del programa
Unidad 1
Unidad 1
PriorizaciónUnidad 1
PriorizaciónUnidad 1
PriorizaciónUnidad 1
Indicadores
Indicadores unidad 1
- -Aplican la propiedad distributiva de la multiplicación en productos de sumas.
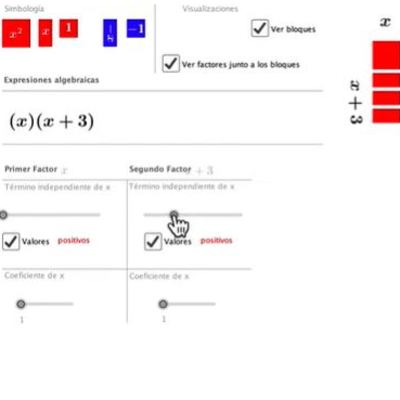
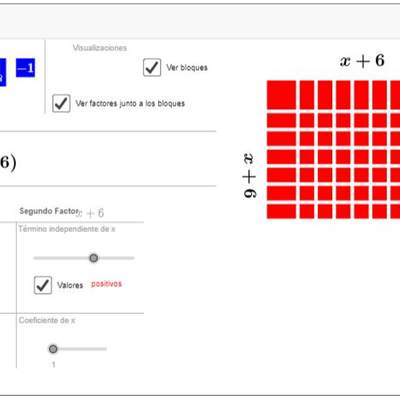
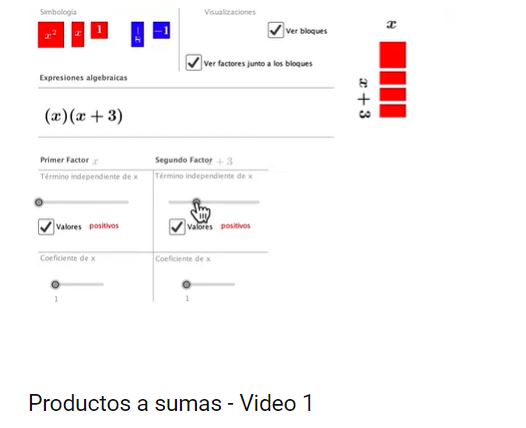
- -Representan los tres productos notables mediante la composición y descomposición de cuadrados y rectángulos.
- -Reconocen los productos notables como caso especial del producto de dos sumas o diferencias.
- -Reconocen la estructura de los productos notables en su expresión aditiva.
- -Aplican los productos notables en el desarrollo de expresiones algebraicas.
- -Aplican los productos notables en la factorización y la reducción de expresiones algebraicas a situaciones concretas.
- -Aplican la estructura de los productos notables para completar sumas, al cuadrado de una adición.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Producto notable
Enunciado
Si se sabe que $ab=2$ y que $a^2+b^2=5$, ¿cuál es el valor de $(a-b)^2$?
Alternativas
A) $1$
B) $2$
C) $3$
D) $5$
Producto notable
Enunciado
Un triángulo tiene una base igual a $a-b$ y una altura de $2(a-b)^2$. Entonces, su área es:
Alternativas
A) $2a^3+6a^2b+6ab^2+2b^3$
B) $2a^3-6a^2b+6ab^2-2b^3$
C) $a^3+3a^2b+3ab^2+b^3$
D) $a^3-3a^2b+3ab^2-b^3$
DESAFÍO: Operatoria Algebraica
Enunciado
Si el inverso multiplicativo de $p$ es $\left(1+\dfrac{m}{n}\right)$ y $m\neq -n$, entonces la expresión $p(m^2 -n^2 )$ es equivalente a:
Alternativas
A) $n(m-n)$
B) $n(m+n)$
C) $-\dfrac{m^2-n^2}{n}$
D) $\dfrac{(m^2-n^2)(m+n)}{n}$
Productos notables en la factorización
Enunciado
La siguiente figura muestra dos cuadrados, uno de lado $a$ y otro de lado $b$. ¿Cuál es el área total de la zona gris?
Alternativas
A) $(a+b)^{2}$
B) $(a-b)^{2}$
C) $a^{2}+b^{2}$
D) $(b-a)(b+a)$
Productos notables en la factorización 1
Enunciado
El rectángulo de la figura tiene lados de $20$ y $5$ unidades, respectivamente. ¿Cuál es el área de la región achurada?
Alternativas
A) $(10 + 8x)^2$
B) $100 - 16x^2$
C) $(10 - 4x)(10 + 4x)$
D) $(10 - 8x)(10 + 8x)$
Productos notables
Enunciado
Si $x$ es un número real positivo y la figura es un rectángulo.
¿Cuál de las siguientes expresiones algebraicas representa el área del rectángulo?
Alternativas
A) $x^{2}+7x+12$
B) $2x^{2}+9x+7$
C) $x^{2}+12$
D) $2x+7$
Productos notables
Enunciado
Si x es un número real distinto de 1 y de 2, ¿cuál de las siguientes opciones resulta al dividir la expresión $\dfrac{x-1}{x^2-3x+2}$ por la expresión $\dfrac{x^2-3x+2}{x-2}$?
Alternativas
A) $-2$
B) $x + 1$
C) $x - 2$
D) $x^2 - 2$
