Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA08 OA 04
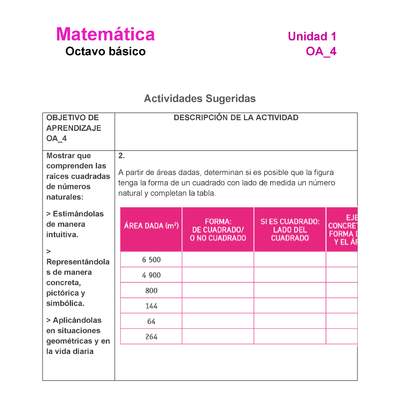
Mostrar que comprenden las raíces cuadradas de números naturales:
- Estimándolas de manera intuitiva.
- Representándolas de manera concreta, pictórica y simbólica.
- Aplicándolas en situaciones geométricas y en la vida diaria.
Clasificaciones
Textos Escolares oficiales 2023

Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 1

Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico

Comprender el significado de la raíz cuadrada de un número positivo
Material didáctico
Lecciones: clases completas
Indicadores
Indicadores Unidad 1
- Estiman en cm, hasta el primer decimal, el largo de un cuadrado cuya área en cm2 no tiene un número cuadrado, y comparan la estimación con multiplicación por sí mismo, utilizando la calculadora.
- Ubican la posición aproximada de raíces no exactas en la recta numérica.
- Resuelven problemas de transformación de rectángulos (u otras figuras 2D) en cuadrados del mismo contenido del área, calculando el lado del cuadrado.
- Calculan el perímetro en situaciones de la vida diaria que involucran cuadrados; por ejemplo: áreas de deporte, escenarios, parques, etc.
- Aplican la raíz cuadrada en la solución de problemas de la vida cotidiana o de ciencias.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Largo de un cuadrado
Enunciado
¿Cuánto mide el lado de un cuadrado cuya área es de $144$ centímetros cuadrados?
Alternativas
A) $36$ centímetros.
B) $72$ centímetros.
C) $12$ centímetros.
D) $18$ centímetros.
Respuesta
C
El área de un cuadrado es lado $\times $ lado, es decir:
lado$^2=144$
lado$=\sqrt{144}$
lado$=12$
Por lo tanto, el lado del cuadrado es $12$ centímetros.
Raíz cuadrada
Enunciado
¿Entre qué pares de números se encuentra $\sqrt{48}$?
Alternativas
A) Entre $4$ y $5$.
B) Entre $6$ y $7$.
C) Entre $0$ y $1$.
D) Entre $8$ y $9$.
Respuesta
B)
$\sqrt{48}$ se encuentra entre $6$ y $7$, ya que:
$6^{2}=36$ y $7^{2}=49$
Con esta información podemos establecer la siguiente relación:
$36<48<49$
$\sqrt{36}<\sqrt{48}<\sqrt{49}$
$6<\sqrt{48}<7$
Largo de un cuadrado
Enunciado
Un cuadrado tiene área $729$ cm$^{2}$. ¿Cuál es el perímetro del cuadrado?
Alternativas
A) $50$ cm
B) $40$ cm
C) $108$ cm
D) $54$ cm
Respuesta
C
Un cuadrado tiene área $729$ cm$^{2}$. Para saber cuánto mide cada lado debemos encontrar la $\sqrt{729}$.
Ahora, sabemos que cada lado tiene un valor de $27$ cm.
Para encontrar el perímetro, sumamos la medida de cada lado; por ende, sumamos $27$ cuatro veces.
El perímetro es:
$27\cdot4=108~\text{cm}$
Raíz cuadrada
Enunciado
¿Entre que pares de números se encuentra la raíz cuadrada de $18$?
Alternativas
A) Entre $1$ y $2$.
B) Entre $3$ y $4$.
C) Entre $4$ y $5$.
D) Entre $5$ y $6$.
Respuesta
C)
$\sqrt{18}$ se encuentra entre $4$ y $5$ ya que:
$4^{2}=16$ y $5^{2}=25$
Con esta información podemos establecer la siguiente relación:
$16<18<25$
$\sqrt{16}<\sqrt{18}<\sqrt{25}$
$4<\sqrt{18}<5$
Perímetros relacionados a cuadrados
Enunciado
Un campo rectangular está formado por dos cuadrados de área $36$ m$^2$ cada uno. ¿Cuál es el perímetro del campo?
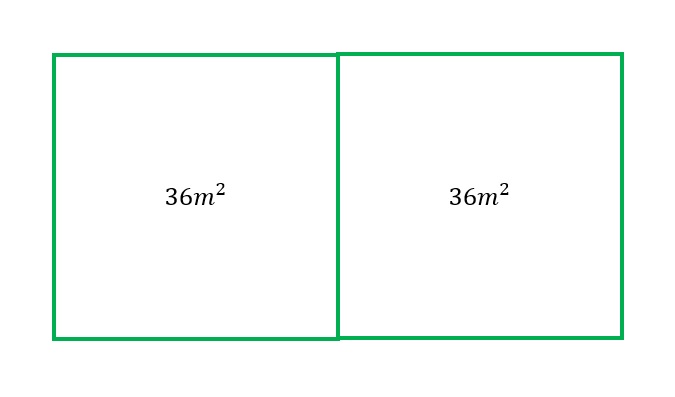
Alternativas
A) $48$ m
B) $36$ m
C) $24$ m
D) $12$ m
Respuesta
B
Cada lado del cuadrado mide $6$ metros; así, el campo tiene dimensiones de $6$ metros por $12$ metros.
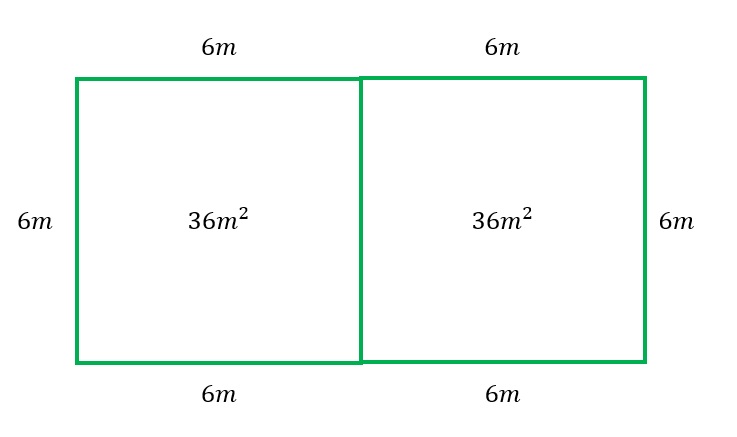
Por lo tanto, su perímetro es:
$6 + 6 + 12 + 12 = 36$ metros.
Transformación de rectangulos
Enunciado
¿Cuál es el largo del lado del cuadrado cuya área es igual que el triángulo rectángulo de la siguiente figura?
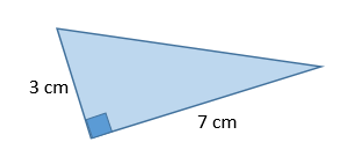
Alternativas
A) $\sqrt{10,5}$ cm
B) $\sqrt{21}$ cm
C) $10,5$ cm
D) $21$ cm
Respuesta
A
El área del triángulo dado es de $10,5$ cm $^2$ . Esto, porque el área del triángulo es $\dfrac{3 \cdot 7}{2}$.
El cuadrado cuya área es $x^2$ cm$^2$ tendrá los lados de $x$ cm. En este caso, el lado del cuadrado de área $10, 5$ cm$^2$ será de largo $\sqrt{10, 5}$, ya que es despejar el valor de $x$:
$$x^2 = 10,5 \Rightarrow x = \sqrt{10,5}$$
Perímetros relacionados a cuadrados
Enunciado
En un parque se desea apartar una zona para que las personas puedan soltar a sus perros. Para esto, es necesario construir una cerca alrededor. La zona delimitada tiene $144$ $m^2$ y debe ser de forma cuadrada. ¿Cuántos metros lineales medirá la cerca que deberán construir?
Alternativas
A) $12$ metros.
B) $24$ metros.
C) $48$ metros.
D) $144$ metros.
Respuesta
C
Cada lado del cuadrado que conforma la zona para las mascotas medirá:
$$\sqrt{144}=12 \text{ metros.}$$.
Como la zona es cuadrada, entonces, tendrá $4$ lados de la misma medida. Por lo que, en total, el perímetro medirá $4 \cdot 12$ metros. Es decir, se deberán construir $48$ metros lineales de cerca.