Inicio - Curriculum Nacional. MINEDUC. Chile.

Enunciado

Un pendrive es un dispositivo pequeño y portátil de almacenamiento de datos informáticos.

Iván tiene un pendrive en el que almacena música y fotos. El pendrive tiene una capacidad de $1$ GB ($1\ 000$ MB). El siguiente gráfico muestra la distribución actual de la capacidad de su pendrive.

$\ $

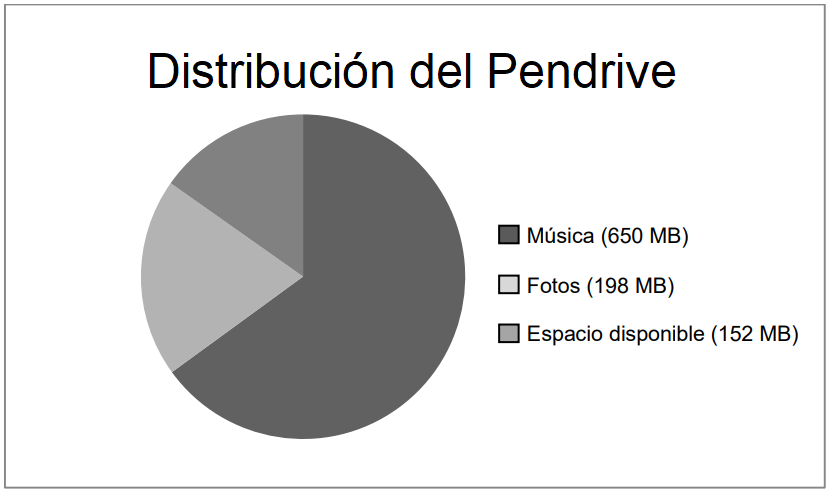
Iván quiere añadir un álbum de fotos de $350$ MB a su pendrive, pero no hay suficiente espacio disponible.
No quiere eliminar ninguna de las fotos, pero no le importaría eliminar hasta dos álbumes de música.

El tamaño de los álbumes de música que Iván tiene almacenados en su pendrive es el siguiente:

$\ $

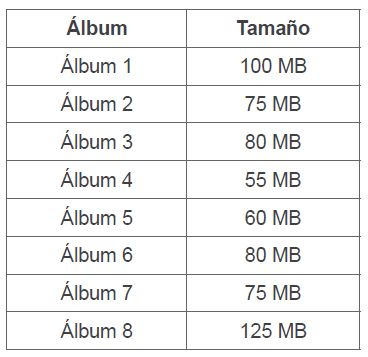
Eliminando dos álbumes de música como máximo ¿tendría Iván suficiente espacio en su pendrive para añadir el álbum de fotos? Encierra "Sí" o "No" en un círculo y muestra tus cálculos para justificar tu respuesta.

Respuesta: $\quad$ Sí $\quad/\quad$ No

Enunciado

Una pelota de goma es lanzada desde un techo de $18$ metros de altura y rebota hasta la mitad de su altura en cada rebote. ¿Cuál es la distancia total que la pelota ha recorrido cuando toca el suelo por tercera vez?

Alternativas

A) $31,5$ m

B) $40,5$ m

C) $\ 45$ m

D) $\ 63$ m

Enunciado

Roberto y Jaime sa repartieron las cerezas de una canasta.

Roberto sacó $\dfrac{1}{3}$ de las cerezas y Jaime sacó $\dfrac{1}{6}$ de las cerezas.

¿Qué fracción de las cerezas quedó en la canasta?

Alternativas

A) $\dfrac{1}{2}$

B) $\dfrac{1}{3}$

C) $\dfrac{1}{6}$

D) $\dfrac{1}{12}$

Enunciado

Para una convivencia se compraron seis pizzas grandes, del mismo tamaño.

En una mesa pequeña se pusieron dos de las pizzas, de las cuales sobró la mitad de una.

En una mesa grande se pusieron las pizzas restantes, y sobró la cuarta parte de una pizza.

En el siguiente espacio, haz la matematica necesaria para determinar qué fracción de las pizzas se consumieron durante la convinencia.

$\ $

La fracción de las pizzas que se comieron es __________.

Enunciado

Una trabajadora va poniendo la uva que cosecha en un tonel. Primero llena $\dfrac{1}{4}$ del tonel y después llena $\dfrac{1}{8}$ más del tonel. ¿Qué fracción del tonel le queda por llenar?

Alternativas

A) $\dfrac{1}{8}$

B) $\dfrac{5}{8}$

C) $\dfrac{2}{12}$

D) $\dfrac{1}{32}$

Enunciado

Ximena compró $4$ kg de harina porque quiere hacer $3$ queques. Para hacer un queque se necesita $\dfrac {3}{4}$ kg de harina.

Si Ximena hace los $3$ queques, ¿cuánta harina le sobrará?

Alternativas

A) $\large 1 \frac{3}{8}$ kg

B) $\large 1 \frac{3}{4}$ kg

C) $\large 2 \frac{1}{4}$ kg

D) $\large 2 \frac{3}{8}$ kg

Enunciado

Dos tercios de las personas presentes al comienzo de una reunión son hombres. Nadie se va y llegan 10 hombres y 10 mujeres a la reunión.

¿Cuál de las siguientes afirmaciones es verdadera?

Alternativas

A) Hay más hombres que mujeres en la reunión.

B) Hay más mujeres que hombres en la reunión.

C) Hay la misma cantidad de hombres que de mujeres en la reunión.

D) Con la información entregada, no se puede saber si hay más mujeres o más hombres en la reunión.