Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA2M OA 11
Utilizar permutaciones y la combinatoria sencilla para calcular probabilidades de eventos y resolver problemas.
Clasificaciones
Textos Escolares oficiales 2023
Actividades de apoyo pedagógico
Lecciones: clases completas
Evaluaciones del programa
Indicadores
Indicadores unidad 4
- -Realizan permutaciones de hasta cinco elementos, con material concreto o pictóricamente.
- -Reconocen el patrón con el cual se aumenta el total de posibilidades si se agrega un elemento.
- -Aplican el término "n!" en la resolución de problemas azarosos.
- -Combinan las permutaciones con el sorteo al azar, con o sin reposición.
- -Resuelven problemas de juegos de azar y de la vida cotidiana, aplicando combinatoria y permutaciones.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Permutaciones
Enunciado
En una carrera de atletismo participarán $10$ estudiantes de II medio y se repartirán medallas diferentes a los $3$ primeros que crucen la meta. ¿De cuántos modos distintos pueden repartirse las medallas?
Alternativas
A) $720$ modos.
B) $620$ modos.
C) $25$ modos.
D) $103$ modos.
Respuesta
A
En la situación se nos presenta una variación de $10$ elementos tomados de $3$ en $3$, donde se nos pide formar grupos de $3$ individuos, de un total de $10$ personas, importando el orden y sin repetir. De esta forma, puede modelarse mediante una permutación de $10$ elementos en grupos de $3$.
$P_{10 3}=\dfrac{10!}{(10-7)!}= \dfrac{10!}{(7)!}= \dfrac{10 \cdot 9 \cdot 8 \cdot 7!}{7!}= 10 \cdot 9 \cdot 8 = 720$
Por lo tanto, pueden ordenarse de $720$ modos distintos.
Aplicación de "n!"
Enunciado
¿Cuántas expresiones de $5$ letras pueden formarse con las vocales: A, E, I, O, U, sin que estas se repitan?
Alternativas
A) $3 125$ expresiones.
B) $120$ expresiones.
C) $5$ expresiones.
D) $25$ expresiones.
Respuesta
B)
En la situación que se presenta, se nos pide formar expresiones de $5$ elementos, sin repetirlos. De esta forma, puede modelarse mediante una permutación sin repetición.
$n=5$
El total de expresiones sera:
$n!=5!=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$
Banco de Preguntas [Banco de preguntas-MA2M OA11-1050619] Matemática 2M
Enunciado
En una carrera participan $5$ competidores. ¿De cuántas formas diferentes pueden repartirse los premios si existen solo primer, segundo y tercer lugar?
Alternativas
A) $5!$
B) $\dfrac{5!}{2!}$
C) $\dfrac{5!}{(5-3)!3!}$
D) $\dfrac{5!}{3!}$
Respuesta
B
Se quiere ordenar $3$ premios (por lo tanto el orden importa) en un total de $5$ competidores (no todos los elementos entran en el ordenamiento). Por lo tanto, se está frente a una variación sin repetición (dado que dos premios no pueden ser asignados a un mismo competidor; es decir, no se repiten), de un total de $5$ elementos en un grupo de $3$.
La fórmula para la variación sin repetición es:
$$\dfrac{n!}{(n-k)!}$$
donde $n$ representa el total de elementos y $k$ el tamaño del grupo en el que se quieren ordenar.
Es decir, $n=5$ y $k=3$. Reemplazando en la fórmula se obtiene:
$$\dfrac{5!}{2!}$$
Otra forma de resolverlo es pensar que el primer premio puede ser entregado a uno de los $5$ participantes. Una vez asignado este premio, solo quedan $4$ posibles ganadores del segundo premio y luego, $3$ posibles ganadores del tercero (ya que los otros dos premios están asignados).
Utilizando principio multiplicativo multiplicamos:
$$5 \times 4 \times 3=\dfrac{5!}{2!}$$
Skateboard
Enunciado
Eric es un fanático del skateboard. Visita una tienda para comprobar algunos precios.
En la tienda se puede comprar un skate completo. También se puede comprar una tabla, un juego de $4$ ruedas, un juego de dos ejes y un juego de accesorios, por separado, para armar el skate uno mismo.
La tienda ofrece $3$ tipos de tablas, $2$ tipos de ruedas y $2$ tipos de accesorios. Solo hay una opción para el juego de ejes.
¿Cuántos skates distintos puede armar Eric?
Alternativas
A) $6$
B) $8$
C) $10$
D) $12$
Respuesta
D
Pizzeria
Enunciado
En una pizzería, los clientes pueden crear su propia pizza. La Pizzería ofrece una pizza con dos ingredientes básicos: queso y tomate. Además, se puede elegir entre diferentes ingredientes adicionales.
Raúl desea ordenar una pizza con dos ingredientes adicionales. La Pizzería ofrece cuatro diferentes ingredientes adicionales: aceitunas, jamón, champiñones y salame.
¿Cuántas combinaciones diferentes puede elegir Raúl?
RESPUESTA: ________ combinaciones.
Respuesta
6
Ping-Pong
Enunciado
Tomás, Roberto, Bernardo y Daniel formaron un grupo de entrenamiento en un club de ping-pong. Cada jugador desea jugar una vez contra cada uno de los otros jugadores. Ellos reservaron dos mesas de entrenamiento para sus partidos.
Completa el siguiente programa de partidos escribiendo el nombre de los jugadores en cada partido.
| Mesa de entrenamiento 1 | Mesa de entrenamiento 2 | |
| Turno 1 | Tomás - Roberto | Bernardo - Daniel |
| Turno 2 | ||
| Turno 3 |
Respuesta
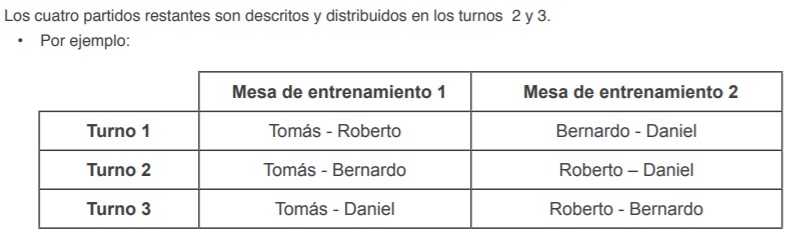 .
.
Banco de Preguntas [Banco de preguntas-MA2M OA11-149] Matemática 2M
Enunciado
La figura muestra un estacionamiento visto desde arriba, donde los rectángulos representan las entradas y los círculos las salidas:

¿De cuántas maneras distintas un conductor puede entrar y salir del estacionamiento?
Alternativas
A) 3
B) 4
C) 7
D) 12
Respuesta
D
Al ingresar por cualquiera de las entradas, el conductor puede tomar 3 salidas distintas por lo tanto las posibles combinaciones son:
4$\cdot$ 3 = 12
Combinatoria y permutaciones
Enunciado
En un barco hay n banderas de igual forma y tamaño, de las cuales una es roja, una es amarilla y el resto son azules. ¿Cuál de las siguientes expresiones representa el total de formas distintas en que se pueden ordenar todas las banderas en una línea?
Alternativas
A) n $\cdot$ (n - 1)
B) $\dfrac{n\cdot(n-1)}{2}$
C) n - 2
D) $\dfrac{n-2}{2}$
Respuesta
A)
Como nos importa el orden en el que queden las banderas, no tomamos todo los elementos (la bandera roja y la amarilla) y, ademas, no podemos repetirlas; lo que tenemos que calcular es la variación de n elementos tomados de 2 en 2, es decir:
$\dfrac{n!}{(n-2)!}$
n(n - 1)
Aplicación de "n!"
Enunciado
En un automóvil viajarán 5 personas. Si sólo uno de ellos sabe conducir, por lo que se ubicará en el asiento del chofer, ¿de cuántas formas distintas se pueden ubicar las cuatro personas restantes?
Alternativas
A) 120
B) 24
C) 16
D) 12
Respuesta
B
Dado que una de las personas está fija, debemos ordenar sólo 4 personas, por lo que se trata de una permutación de 4 elementos.
Luego, el resultado es:
4! = 24
Combinatoria y permutaciones
Enunciado
Alejandra va a una tienda a comprarse un vestido. Cuando esta ahí observa los seis modelos distintos que hay para elegir. Si decide comprar dos vestidos, ¿de cuántas maneras distintas se puede hacer esta selección?
Alternativas
A) 1
B) 3
C) 6
D) 15
Respuesta
D
Para calcular de cuántas maneras distintas podemos combinar los seis vestidos diferentes, debemos tener claro que no se pueden repetir y que el orden en que los combinemos no importa.
Por lo tanto, esto es una combinatoria sin repetición y la expresión que nos permite determinar tal cantidad está dada por:
C = $\displaystyle\frac{n!}{r!\ (n-r)!}$
donde n corresponde a la cantidad de trajes y r a la cantidad que queremos escoger.
Por lo tanto, la cantidad de combinaciones de 2 vestidos posibles es:
$\displaystyle\dfrac{6!}{2!\cdot(6-2)!}=\dfrac{6!}{2!\cdot 4!}=\dfrac{720}{2\cdot 24}=\dfrac{720}{48}$ = 15
Banco de Preguntas [Banco de preguntas-MA2M OA11-23767] Matemática 2M
Enunciado
Se tienen 5 llaves que se quiere distribuir en dos llaveros (uno dorado y otro plateado), de tal forma que en el llavero dorado queden 3 llaves. ¿De cuántas formas se pueden elegir las llaves que irán en el llavero dorado?
Alternativas
A) $3$
B) $5$
C) $10$
D) $15$
Respuesta
C
Para saber las combinaciones totales de elecciones de llaves utilizamos una combinatoria, debido a que se debe escoger solamente la cantidad indicada, entonces:
$\dfrac{5!}{(5-3)!\cdot{3!}}$ = $\dfrac{5\cdot4}{2\cdot1}$ = $5\cdot2$
Formando números
Enunciado
¿Cuántos números diferentes se pueden escribir con los dígitos 3, 3, 3, 4, 4, 4, 4, utilizándolos todos?
Alternativas
A) 7
B) 35
C) 70
D) 210
Respuesta
B
Formando palabras
Enunciado
¿Cuántas palabras, con o sin sentido, que comienzan con L, se pueden formar con las letras de la palabra HELADO?
Alternativas
A) 720
B) 120
C) 24
D) 15
Respuesta
B
Palabras con restricciones
Enunciado
¿Cuántas palabras de tres letras, con o sin sentido, se pueden formar con las letras de la palabra LABIOS, si sólo las dos primeras letras deben ser vocales?
Alternativas
A) 18
B) 27
C) 75
D) 120
Respuesta
A
Se necesitan cantantes
Enunciado
El director de un coro profesional publica un aviso en el diario:
Se requiere una primera voz, una segunda voz y una tercera voz para un coro que interpreta música rock. Los cantantes interesados deben presentarse a una audición. A la audición se presentan 8 cantantes, ¿de cuántas maneras se pueden elegir las tres voces?
Alternativas
A) 6 maneras.
B) 56 maneras.
C) 336 maneras.
D) 512 maneras.
Respuesta
C
Una foto
Enunciado
Los ocho jugadores de un equipo de básquetbol y su entrenador desean sacarse una fotografía. La foto será de pie y ordenados en fila, de modo que el entrenador quede al centro de los jugadores. ¿De cuántas maneras diferentes se pueden ordenar en la foto?
Alternativas
A) $4!\;+\;4!$
B) $4!\;+\;1!\hspace{0,3cm}4!$
C) $8!$
D) $9!$
Respuesta
C
¿Vamos al circo?
Enunciado
Felipe se ha ganado 5 entradas para ir al circo. Si tiene 9 amigos con quienes poder ir, ¿de cuántas maneras diferentes puede escoger Felipe a los 4 amigos que lo acompañarán al circo?
Alternativas
A) 126
B) 256
C) 630
D) 1.260
Respuesta
A
















