Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA2M OA 03
Mostrar que comprenden la función cuadrática f(x)= ax2 + bx + c (a ≠ 0):
- Reconociendo la función cuadrática f(x) = ax2 en situaciones de la vida diaria y otras asignaturas.
- Representándola en tablas y gráficos de manera manual y/o con software educativo.
- Determinando puntos especiales de su gráfica.
- Seleccionándola como modelo de situaciones de cambio cuadrático de otras asignaturas, en particular de la oferta y demanda.
Clasificaciones
Textos Escolares oficiales 2023
Actividades de apoyo pedagógico
Material didáctico
Lecciones: clases completas
Evaluaciones del programa

Evaluación Programas - MA2M OA03 - U2 - FUNCIÓN CUADRÁTICA EN LA VIDA DIARIA
Indicadores
Indicadores unidad 2
- -Reconocen representaciones de la función cuadrática en curvas de la vida cotidiana (balísticas, caída de pelotas, caída de agua, etc.).
- -Grafican funciones cuadráticas a partir de una tabla de valores en la cual están dados los diferentes parámetros a, b, c.
- -Elaboran gráficos de la función f(x) = ax2 + bx + c, considerando a > 0 o a < 0 (variando respectivamente b y c).
- -Grafican y derivan la función para distintos valores de sus parámetros, obteniendo la forma canónica y = a(x - d)2 + e.
- -Analizan las variaciones de la gráfica mediante diferentes medios de representación.
- -Marcan y encuentran numéricamente la intersección de la gráfica de la función f(x) = ax2 + bx + c, con el eje x.
- -Determinan en el plano cartesiano las regiones cuyos puntos P(x,y) representan soluciones (x,y) de las inecuaciones cuadráticas y < ax2 + bx + c o y > ax2 + bx + c.
- -Modelan situaciones de cambio cuadrático de la vida cotidiana y de las ciencias, por medio de la función cuadrática.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Gráfica función cuadrática
Enunciado
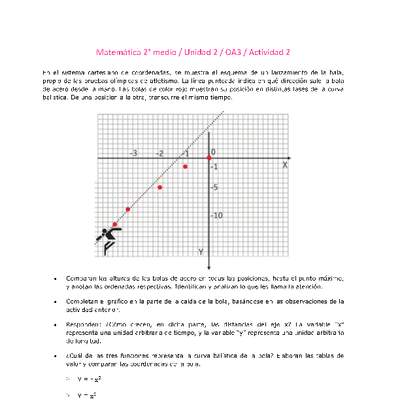
En la figura se muestra una función cuadrática, la cual representa las ganancias de una empresa por la venta de un producto. El eje X representa el número de docenas vendidas y el eje Y representa las ganancias expresadas en miles de pesos.

Si se sabe que el vértice de la función es $\mbox{(25; 56,5)}$, ¿cómo se comporta la función cuando se venden más de $25$ docenas del producto?
Alternativas
A) Las ganancias comienzan a decrecer.
B) Las ganancias comienzan a crecer.
C) La empresa no tiene pérdidas ni ganancias.
D) La ganancia es nula.
Respuesta
A
Debemos analizar la información presentada.
- Representación Eje X: Número de docenas vendidas.
- Representante del Eje Y: Ganancias de la empresa.
El vértice (punto máximo) de la función está en $ (25; 56,5) $, por lo tanto, cuando se venden más de $ 25 $ docenas (rama derecha de la función cuadrática) las ganancias comienzan a decrecer.
Intersección de funciones con el eje x
Enunciado
¿En cuál de los siguientes puntos la gráfica de la función $f(x)=x^2-10x+25$ intersecta al eje X?
Alternativas
A) $(-5,0)$
B) $(5,0)$
C) $(25,0)$
D) $(-25,0)$
Respuesta
B)
Veamos que:
$ x^2-10x+25=0$
$(x-5)(x-5)=0$
$x=5$
Por lo tanto, la gráfica de $f$ intersecta al eje $X$ en el punto $(5,0)$.
Banco de Preguntas [Banco de preguntas-MA2M OA03-16292] Matemática 2M
Enunciado
Sea $f(x)=\sqrt{4-x^2}$ una función real. El dominio de la función es el conjunto:
Alternativas
A) $[\ 2, \infty[$
B) $[-2, 2\ ]$
C) $]-\infty, 2\ ]$
D) $]-\infty, 2\ [$
Respuesta
B
La función está definida en los reales, por lo tanto, el dominio es un subconjunto de los reales. Debe cumplirse que:
$4-x^{2}\geq 0 \Longrightarrow x^2\leq 4 \Longrightarrow |x|\leq 2$.
Por lo tanto, si $x\in\ [-2, 2\ ]$, la función estará bien definida.
Función cuadrática en lo cotidiano
Enunciado
La altura (medida en metros) alcanzada por una pelota lanzada al aire es modelada con la función $f(x) = \displaystyle \frac{x^{2}+1}{3} $. Determina la altura de la pelota a los $2$ segundos después de haberla lanzado.
Alternativas
A) $ \dfrac{2}{3} m$
B) $ -\dfrac{1}{3} m$
C) $ \dfrac{5}{3}m $
D) $ -\dfrac{5}{3} m$
Respuesta
D
Para resolver el problema se debe reemplzar el valor de $x$ en la función por $-2$, con lo que se obtiene lo siguiente:
$ f(-2) = \displaystyle \frac{\left(-2\right)^{2} +1}{3} =\displaystyle \frac{5}{3}$
Banco de Preguntas [Banco de preguntas-MA2M OA03-22759] Matemática 2M
Enunciado
¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s) con respecto al gráfico de la función $f(x)=ax^2 + bx + c$?

I. El valor de $a$ es negativo.
II. $b=c=0$.
III. $b+c=1$.
Alternativas
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
Respuesta
D
El valor de $a$ en una ecuación cuadrátrica nos indica la concavidad de la parábola; es decir, si $a > 0$, entonces, la parábola abre hacia arriba. Por el contrario, si $a < 0$, la parábola abre hacia abajo.
Como la parábola no corta la eje $X$, excepto en el 0, entonces, $b = c = 0$.
Por lo tanto, solo las afirmaciones I y II son correctas.
Gráfica función cuadrática
Enunciado
La figura muestra la representación gráfica de una función cuadrática de la forma $f(x) = ax^2 + bx + c$, con $a$, $b$ y $c \in \mathbb{R}$ y $a\ne 0$.

Al respecto, ¿cuál(es) de las siguientes afirmaciones es (son) siempre verdadera(s)?
I. La función está definida para todo $\mathbb{R}$.
II. El discriminante de la función es mayor que $0$.
III. El valor de $c$ es $2$.
Alternativas
A) Solo I
B) Solo II
C) Solo III
D) I, II y III
Respuesta
D)
Veamos cada una de las afirmaciones:
I. La gráfica de la función nos dice que el conjunto de sus preimágenes (su dominio) lo conforman los números negativos y positivos, pasando por el cero. Puesto que, además, la gráfica de $f$ es continua (se dibuja con un solo trazo continuo), se concluye que su dominio son los números reales.
II. Como la gráfica de la función tiene dos raíces (corta en dos puntos al eje de las abcsisas), el discriminante de la función es mayor que cero.
III. $c$ corresponde al punto de intersección de la función con el eje ordenado cuando $x$ toma valor $0$. En la gráfica podemos observar que dicha intersección ocurre en $y=2$, de modo que se cumple que $c=2$.
Por lo tanto, las afirmaciones I, II y III son siempre correctas.
Banco de Preguntas [Banco de preguntas-MA2M OA03-23417] Matemática 2M
Enunciado
Sea $g(x)$ una función de la forma $ax^2+bx+c$ con $a b c \in \mathbb{R}$ y $a \neq 0$. Se puede asegurar que la gráfica de $g$ intercepta en dos puntos al eje de las abcisas, si se sabe que:
(1) $a > 0$
(2) $b > 0$
Alternativas
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas (1) y (2).
D) Se requiere información adicional.
Respuesta
D
La función $ax^2+bx+c$ con $a b c \in \mathbb{R}$ interceptará dos veces al eje de las abscisas si $b^2-4ac > 0$ o, de otra forma, $b^2 > 4ac$.
$a > 0$ y $b > 0$ no asegura que $b^2 > 4ac$ y resulta necesario el valor de $c$.
Por lo anterior, se necesita información adicional.
Intersección de funciones con el eje x
Enunciado
¿En cuál de las siguientes gráficas se representan mejor las funciones:
f(x) = x - 2
g(x) = x$^2$ - x - 2?
Alternativas

Respuesta
D)
Veamos que y = x - 2 luego la pendiente es positiva y con esto descartamos la opción A y B ya que en esos gráficos se presenta una recta de pendiente negativa.
La recta corta al eje y en -2 esto está representado en las alternativas C y D.
De la segunda ecuación la coordenada x del vértice de la parábola es:
$\displaystyle \frac{-b}{2a}$ = $\displaystyle \frac{1}{2}$
y con esto descartamos la alternativa C ya que pareciera que el eje de simetría está en el lado de los negativos.
Buscando el vértice
Enunciado
Sea la función cuadrática
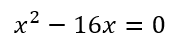
¿Cuál de los siguientes puntos corresponde al vértice de la gráfica?
Alternativas
A) $V(8,16)$
B) $V(-8,64)$
C) $V(-8,-6)$
D) $V(8,-64)$
Respuesta
D)
Ceros de una función cuadrática
Enunciado
Sea la función $f(x) = x^2 - 10x + 24$. ¿Cuáles son los ceros de la función?
Alternativas
A) $(-12,0) y (-2,0)$
B) $(6,0) y (4,0)$
C) $(0,6) y (0,4)$
D) $(0,12) y (0,2)$
Respuesta
B)
Reconociendo una función cuadrática
Enunciado
Dada la función $f(x) = x^2 + 3x - 4$, ¿cuál de los siguientes gráficos se asocia con esta función?
Alternativas
A) 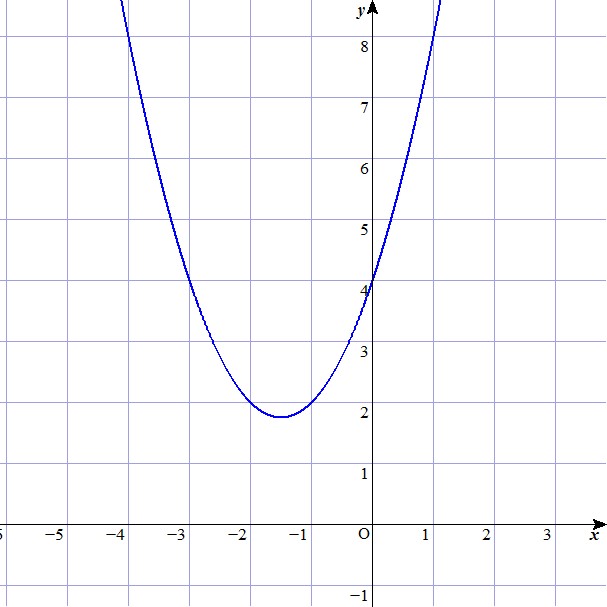
B) 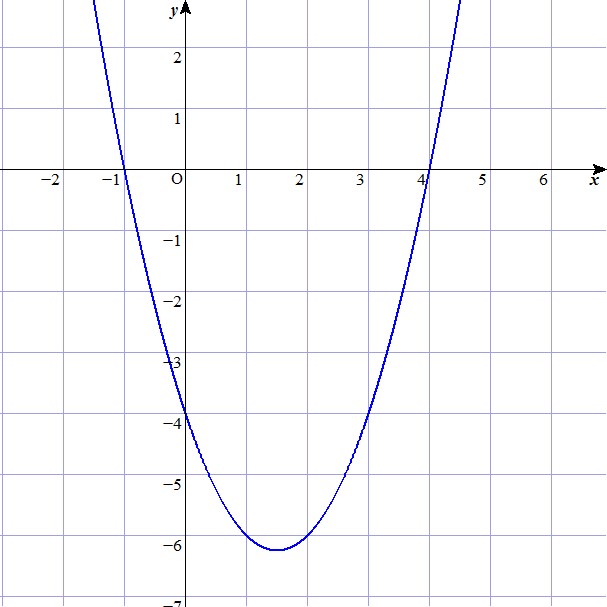
C) 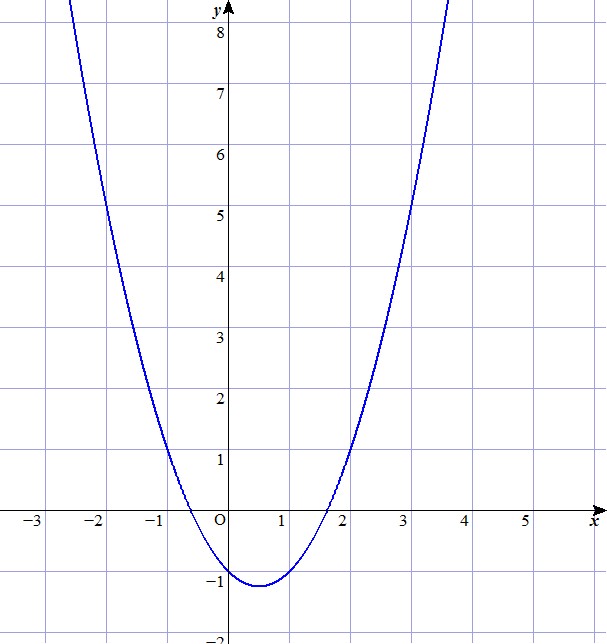
D) 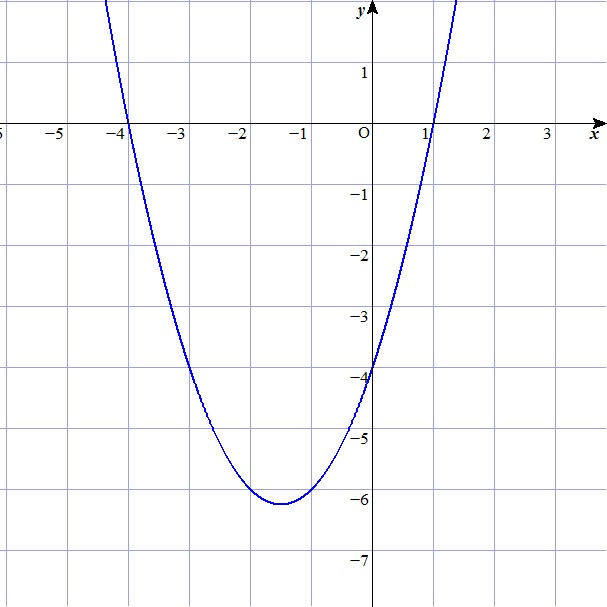
Respuesta
D
Reconociendo una función cuadrática
Enunciado
¿Cuál de las siguientes tablas de valores de funciones cuadráticas representa una función cuadrática con concavidad positiva?
Alternativas
Respuesta
B)
DESAFIO: Manzanos
Enunciado
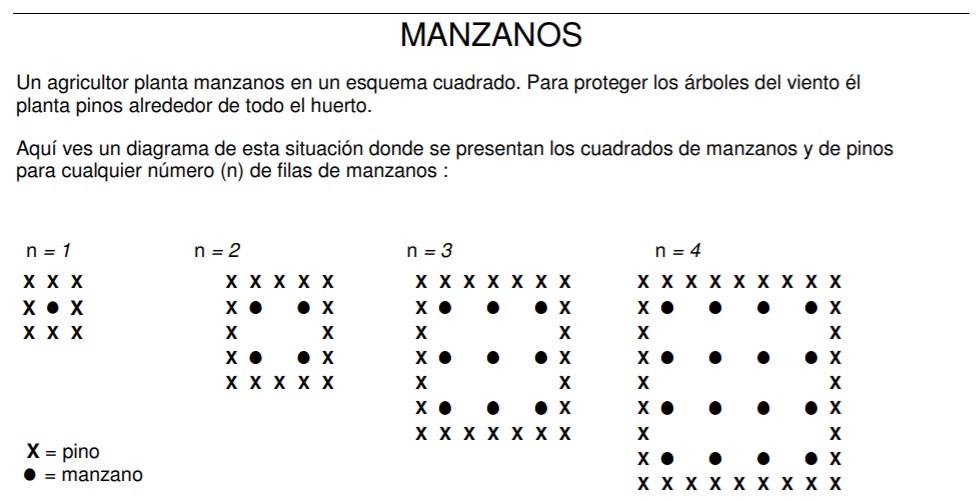
El agricultor quiere hacer un huerto mucho más grande con muchas filas de árboles. A medida que el agricultor agranda el huerto ¿qué aumentará más rápidamente: el número de manzanos o el número de pinos? Explica como encontraste tu respuesta.

Respuesta
Puntaje completo:
La respuesta correcta (manzanos) acompañada de una explicación válida. Por ejemplo:
- Manzanos = $n \cdot n$ y los pinos = $8 \cdot n$ ambas fórmulas tienen un factor $n$ pero los manzanos tienen otra $n$ la cual hace que sea más grande donde el factor 8 es el mismo. El número de manzanos se incrementa más rápidamente.
- El número de manzanos se incrementa más rápido porque está al cuadrado en vez de estar multiplicado por 8.
- El número de manzanos es al cuadrado. El número de pinos es lineal. Por lo tanto los manzanos se incrementarán más rápido.
- Usa gráficos para contestar que $n^{2}$ es mayor que $8n$ después de $n=8$.
[Nota que el puntaje completo se da si el estudiante proporciona algunas explicaciones algebraicas basadas en la fórmula $n^{2}$ y $8n$.
Puntaje parcial:
Respuesta correcta (manzanos) basada sobre ejemplos específicos o sobre el desarrollo de la tabla.
- La cantidad de manzanos se incrementará más rápidamente porque si usamos la tabla (de la página anterior) encontramos que la cantidad de manzanos se incrementa más rápido que la cantidad de pinos. Esto pasa especialmente después de que la cantidad de manzanos y pinos es la misma.
- La tabla muestra que la cantidad de manzanos se incrementa más rápidamente.
O
Respuesta correcta (manzanos) con ALGUNA evidencia que es entendida la relación $n^{2}$ y $8n$ pero no es claramente expresada como en las respuestas de puntaje completo.
- Los manzanos después de que $n > 8$.
- Después de 8 filas la cantidad de manzanos se incrementará más rápidamente que la de pinos.
- Los pinos hasta que haya 8 hileras entonces serán más manzanos.