Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA1M OA 01
Calcular operaciones con números racionales en forma simbólica.
Clasificaciones
Textos Escolares oficiales 2023

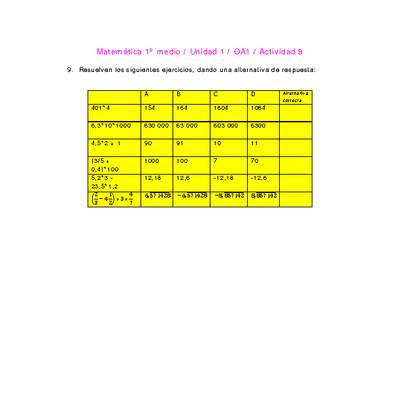
Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 1

Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico

Planificación y Gestión de las Finanzas - Tópico Generativo
Indicadores
Indicadores unidad 1
- -Identifican el tipo de número, racional, entero y natural, y las operaciones involucradas.
- -Realizan operaciones mixtas con números racionales, respetando la jerarquía de las operaciones y los paréntesis.
- -Reducen expresiones numéricas de números racionales, aplicando las propiedades de conmutatividad, asociatividad y distributividad.
- -Transforman expresiones del lenguaje natural a expresiones matemáticas y viceversa.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Conjuntos numéricos y operaciones
Enunciado
$1,{ }\overline{6} + 0,{ }\overline{3} - \dfrac{2}{3} = $
Alternativas
A) $\dfrac{-13}{9}$
B) $\dfrac{4}{3}$
C) $\dfrac{37}{30}$
D) $\dfrac{3}{4}$
Respuesta
B
Primero se procede a transformar los decimales periódicos a fracción; es decir:
- $1,{ }\overline{6} = \dfrac{16-1}{9} = \dfrac{15}{9} = \dfrac{5}{3}$
- $0,{ }\overline{3} = \dfrac{3-0}{9} = \dfrac{3}{9} = \dfrac{1}{3}$
Veamos que al desarrollar obtenemos:
$ 1,{ }\overline{6}+0,{ }\overline{3}-\dfrac{2}{3} = \dfrac{5}{3} + \dfrac{1}{3} - \dfrac{2}{3} = \dfrac{5+1-2}{3} = \dfrac{4}{3}$
Jerarquía en operaciones mixtas
Enunciado
El resultado de $\left(\displaystyle\frac{1}{7}\cdot\displaystyle\frac{21}{3}+4\right):\displaystyle\frac{2}{3}$ es:
Alternativas
A) $\displaystyle\frac{15}{2}$
B) $\displaystyle\frac{12}{2}$
C) $\displaystyle\frac{15}{3}$
D) $\displaystyle\frac{10}{3}$
Respuesta
A
Para resolver este ejercicio es necesario realizar las operaciones en el orden correcto. Primero el paréntesis; dentro de él encontramos una multiplicación y una suma: primero se debe multiplicar y luego sumar. En este caso tenemos que:
$$\left(\displaystyle\frac{1}{7}\cdot\displaystyle\frac{21}{3}+4 \right) = \left(\displaystyle\frac{1\cdot21}{7\cdot3}+4 \right) = \left(\displaystyle\frac{21}{21}+4 \right)=(1+4) = 5$$
Luego, debemos resolver la división:
$$5:\displaystyle\frac{2}{3} = 5\displaystyle\cdot\frac{3}{2} = \displaystyle\frac{5}{1}\cdot\displaystyle\frac{3}{2} =\displaystyle\frac{5\cdot3}{1\cdot2} = \displaystyle\frac{15}{2}$$
Jerarquía en operaciones mixtas
Enunciado
Si $x = y^2;~ y = \displaystyle \frac{5}{k}$; entonces, ¿cuál es el valor de $x$ cuando $k =\displaystyle \frac{1}{2}$?
Alternativas
A) $\dfrac{5}{2}$
B) $50$
C) $20$
D) $100$
Respuesta
D
Veamos que:
$$y=\displaystyle\frac{5}{k} \text{ si } k=\displaystyle\frac{1}{2} \rightarrow y=\displaystyle\frac{5}{\dfrac{1}{2}} =5\cdot 2=10$$
$$x=y^2 \text{ pero } y=10 \rightarrow x=10^2=100$$
Conjuntos numéricos y operaciones
Enunciado
$0,{ }\overline{2} + 0,{ }\overline{3} =$
Alternativas
A) 0,5
B) 0,55
C) $\dfrac{5}{9}$
D) $\dfrac{9}{5}$
Respuesta
C
Primero, para hacer más sencillos los cálculos, transformamos los decimales en fracciones:
$0,{ }\overline{2} = \dfrac{2}{9}$ y $0,{ }\overline{3}= \dfrac{3}{9}$
Luego:
$0,{ }\overline{2} + 0,{ }\overline{3} = \dfrac{2}{9} + \dfrac{3}{9} = \dfrac{5}{9}$
Lenguaje natural y matemático
Enunciado
Si $m = 5$ y $n = 7$; entonces, ¿cuál(es) de las siguientes expresiones representa(n) un número par?
I. $5m+7n$
II. $n(m + 3n) + 2m$
III. $mn + 5n + 3m$
Alternativas
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
Respuesta
D
Resolviendo una a una las afirmaciones obtenemos lo siguiente:
I. $5m+7n = 5(5)+7(7) = 25+49 = 74$ que es par.
II. $n(m+3n)+2m = 7(5+3(7))+2(5) = 7(5+21)+10 = 7(26)+10 = 182+10 = 192$ que es par.
III. $mn+5n+3m = (5)(7)+5(7)+3(5) = 35+35+15 = 85$ que es impar.
Conclusión, solo I y II representan un número par.
RDP decimales y fracciones
Enunciado
Una bebida está compuesta por:
$\dfrac{1}{4}$ de litro de soda.
$0,125$ litros de jugo de naranja.
$\dfrac{1}{16}$ de litro de limón.
El resto del líquido, hasta completar el litro de bebida, es jugo de fresa.
¿Cuánto jugo de fresa lleva el litro de la bebida?
Alternativas
A) $\dfrac{9}{16}$ de litro.
B) $\dfrac{7}{16}$ de litro.
C) $\dfrac{6}{16}$ de litro.
D) $\dfrac{3}{16}$ de litro.
Respuesta
A) $\dfrac{9}{16}$ de litro.
Resolviendo obtenemos:
$\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}=\dfrac{7}{16}$
$1-\dfrac{7}{16}=\dfrac{9}{16}$
Problema Teatro
Enunciado
Hay $890$ personas en un teatro viendo un concierto. Un quinto de las personas son adultos y el resto son niños y niñas. Si hay $58$ niñas más que niños, ¿cuántos niños hay?

$\ $
Hay _________niños.
Respuesta
$890 \cdot \dfrac{1}{5} = 178$
$890 - 178 = 712$
Hay $712$ niños y niñas
$712 - 58 = 654$
$654 : 2 = 327$
Hay $327$ niños.
Suscripción a una revista
Enunciado
Cristian planea suscribirse a una revista. Las dos revistas que le gustan ofrecen $24$ ejemplares.
Cristián lee los siguientes avisos publicados para las revistas:

Zeds son las unidades monetarias en el país de Cristian.
Responde las preguntas que están a continuación (usa el espacio para hacer tus cálculos):

¿Cuál revista es la más barata por los $24$ ejemplares? La revista más barata es _____________.
¿Cuánto más barata es? Es más barata por ________________ zeds.
Respuesta
Revista Zona Joven.
3 zeds más barata.
Bolitas en una bolsa 2
Enunciado
Paty tenía una bolsa de bolitas. Le dio una tercera parte de ellas a Rebeca y luego, de las que quedaban, le dio un cuarto a Juan. A Paty le quedaron $24$ bolitas en la bolsa.
¿Cuántas bolitas había en la bolsa al comienzo?
Alternativas
A) $36$
B) $48$
C) $60$
D) $96$
Respuesta
B) $48$
Rebeca tiene $\dfrac{1}{3}$ de las bolitas, por lo tanto, lo que queda es $\dfrac{2}{3}$ de las bolitas.
Juan tiene un cuarto de lo que queda, por lo tanto, es $\dfrac{1}{4}$ de $\dfrac{2}{3}= \dfrac{1}{4} \cdot \dfrac{2}{3}= \dfrac{1}{6}$.
Luego, entre Rebeca y Juan tiene en total $\dfrac{1}{3} + \dfrac{1}{6}$ de las bolitas, o sea $\dfrac{1}{2}$.
Así, si la mitad la tienen Rebeca y Juan, la otra mitad la tiene Paty y paty quedó con 24 bolitas.
Si la mitad de las bolitas es $24$, quiere decir que al principio tenía $48$ bolitas.