Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA08 OA 13
Describir la posición y el movimiento (traslaciones, rotaciones y reflexiones) de figuras 2D, de manera manual y/o con software educativo, utilizando:
- Los vectores para la traslación.
- Los ejes del plano cartesiano como ejes de reflexión.
- Los puntos del plano para las rotaciones.
Clasificaciones
Textos Escolares oficiales 2023

Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 1

Matemática 8° básico, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico
Material didáctico
Lecciones: clases completas
Evaluaciones del programa
Unidad 3
Indicadores
Indicadores Unidad 3
- Realizan traslaciones en el plano con vectores dados.
- Determinan el vector entre la imagen y la pre- imagen de 2 figuras 2D trasladadas y modelan la traslación y la combinación de traslaciones, por medio de vectores y la suma de ellos.
- Reflexionan figuras 2D según los ejes dados, de manera concreta y pictórica.
- Determinan el eje de reflexión entre la imagen y la pre-imagen de dos figuras 2D.
- Reconocen que la rotación por 180° es una reflexión en un punto, llamado punto de simetría.
- Identifican rotaciones, reflexiones y traslaciones en situaciones cotidianas.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Traslación con vectores en el plano cartesiano
Enunciado
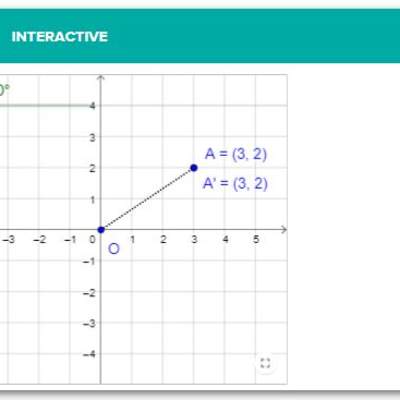
El cuadrilátero de vértices $A (-6,-5)$, $B (-2,-3)$, $C (-3,5)$ y $D (-5,7)$ se trasladó de tal manera que le vértice $D'$, homólogo al vértice $D$, se ubica en la coordenada $(3,3)$.
¿Cuáles son los componentes del vector de traslación $ \vec{t} $?
Alternativas
A) $ \vec{t}\; (8,-4)$
B) $ \vec{t}\; (8,4) $
C) $ \vec{t}\; (8,8) $
D) $ \vec{t}\; (-8,-4) $
Respuesta
A) $ \vec{t}\; (8,-4)$
Supongamos que el vector de traslación es $ \vec{t}\; (a,b)$, entonces tenemos $ (-5+a,7+b)=(3,3)$. Luego igualando coordenadas tenemos:
$-5+a= 3 \wedge 7+b=3$
$a=8 \wedge b=-4$
o también resolver directamente
Primera coordenada del vector = 3-(-5)=8
Segunda coordenada del vector = 3-7=-4
Traslación
Enunciado
Se tiene un triángulo de vértices $A (-2,3)$, $B (1,1)$ y $C (3,5)$, el cual se desplaza según el vector $ \vec{t} (-2,1)$.
¿Cuáles son las coordenadas del $ \Delta A'B'C' $ que se obtiene del $ \Delta ABC $?
Alternativas
A) $A'(4,3), \ B'(-2,1)$ y $C'(-6,5)$
B) $A'(0,4), \ B'(-3,0)$ y $C'(5,4)$
C) $A'(-4,4), \ B'(-1,2)$ y $C'(1,6)$
D) $A'(-4,2), \ B'(-1,0)$ y $C'(-1,4)$
Respuesta
C) $A'(-4,4), \ B'(-1,2)$ y $C'(1,6)$
Si el vector traslación es $\vec{t} (-2,1)$, entonces:
$A (-2,3) = (-2+-2; 1+3)=(-4,4)$
$B (1,1)= (-2+1;1+1)=(-1,2)$
$C (3,5)=(-2+3;1+5)=(1,6)$
Rotaciones, reflexiones y traslaciones
Enunciado
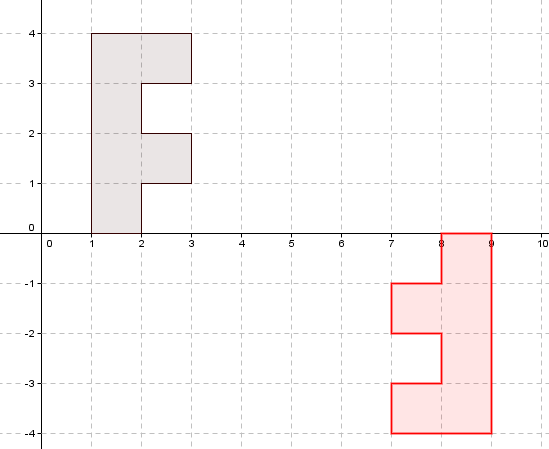
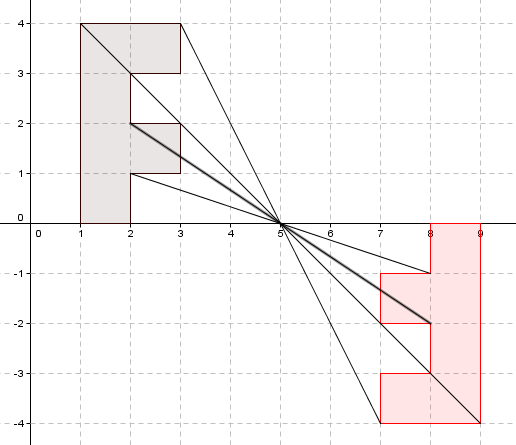
La F que se encuentra sobre la línea del eje de las abscisas ($x$) ha sido rotada obteniéndose la F que se encuentra bajo la línea del eje de las absisas ($x$). ¿Cuál es el centro y ángulo de esta rotación?
Alternativas
A) $(0,5)$ y $90^{\circ}$
B) $(0,0)$ y $180^{\circ}$
C) $(5,0)$ y $90^{\circ}$
D) $(5,0)$ y $180^{\circ}$
Respuesta
D)
En la imagen podemos apreciar que el centro es $(5,0)$ y el ángulo de rotación es $180^\circ$.
Traslaciones
Enunciado
Si $\overrightarrow{A}$ = (-1, 2); $\overrightarrow{B}$ = (-3, -5) y s = $\dfrac{1}{2}$, ¿cuál(es) de las siguientes afirmaciones es(son) verdadera(s)?
I. $\overrightarrow{B} - \overrightarrow{A}$ = (-2, -7)
II. $\overrightarrow{A} + 2\overrightarrow{B}$ = (5, -8)
III. s$\cdot \overrightarrow{A}$ = $\left( -\dfrac{1}{2}, 1\right)$
Alternativas
A) Solo I
B) Solo II
C) Solo I y II
D) Solo I y III
Respuesta
D
Resolviendo cada una de las opciones:
$\overrightarrow{B} - \overrightarrow{A}$ = (-3, -5) - (-1, 2) = (-3 + 1, -5 - 2) = (-2, -7)
$\overrightarrow{A} + 2\overrightarrow{B}$ = (-1 2) + 2$\cdot$ (-3, -5) = (-1, 2) + (-6, -10) = (-7, -8)
s$\cdot \overrightarrow{A}$ = $\dfrac{1}{2}\cdot (-1, 2)$ = $\left(-\dfrac{1}{2}, 1\right)$
Por lo tanto solo I y III son verdaderas.
Traslación por vectores
Enunciado
Respecto a los vectores $\overrightarrow{u}$ = (8, - 6) y $\overrightarrow{v}$ = (- 4, - 3), ¿cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I. $\overrightarrow{u}+\overrightarrow{v}$ = (4, -9)
II. $4\overrightarrow{v}$ = (-16, -12)
III. $-2\overrightarrow{u} + \overrightarrow{v}$ = (-20, -15)
Alternativas
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
Respuesta
D
La primera afirmación es correcta pues:
$\overrightarrow{u}+\overrightarrow{v}$ = (8, -6) + (-4, -3) = (8-4, -6-3) = (4, -9)
La segunda afirmación también es correcta:
$4\overrightarrow{v}$ = 4 $\cdot$ (-4, -3) = (4 $\cdot$ -4, 4 $\cdot$ -3) = (-16, -12)
Por último, la tercera afirmación es falsa puesto que:
$-2\overrightarrow{u} + \overrightarrow{v}$ = -2 $\cdot$ (8, -6) + (-4, -3) = (-16, 12) + (-4, -3) = (-20, 9)
Eje de reflexión
Enunciado
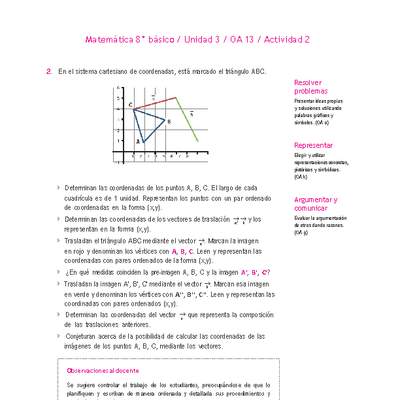
Al punto $P$, de coordenadas $(-1, 4)$, se le aplica una simetría axial con respecto al eje las ordenadas. ¿Cuáles serán las coordenadas del punto imagen de $P$?
Alternativas
A) $(1, 4)$
B) $(1, -4)$
C) $(4, -1)$
D) $(-1, -4)$
Respuesta
A
Una simetría axial es una transformación en la que el punto $P$ se transforma en otro punto $Q$, de modo que el eje dado (en este caso el eje $y$) se transforma en el eje de simetría del segmento $\overline{PQ}$.
Esto se traduce en un cambio, tal que la coordenada en $y$ se mantiene, mientras que la coordenada en $x$ cambia de signo. Luego, $Q=(1, 4)$.
Banco de Preguntas [Banco de preguntas-MA8 OA13-17338] Matemática 8
Enunciado
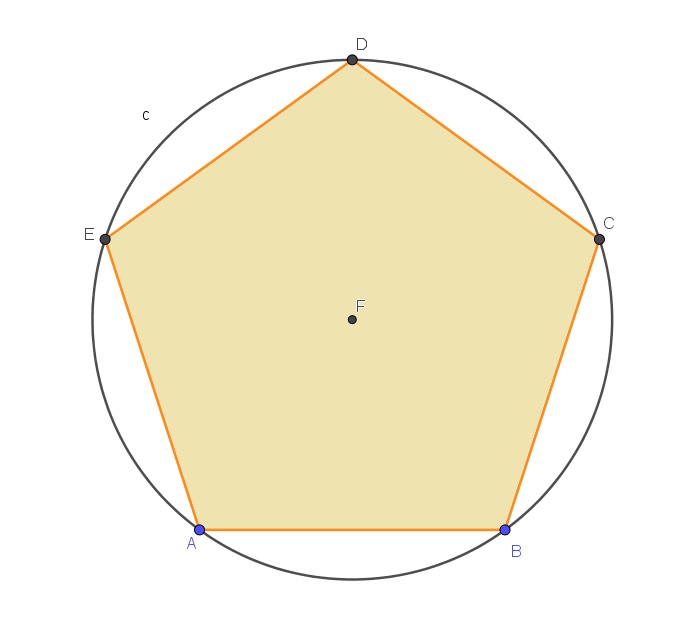
El pentágono regular de la figura se rota en 144$^{\circ}$ en sentido antihorario respecto del centro de la circunferencia F en la que está inscrito. ¿En qué punto de la figura original queda ubicado el vértice A?
Alternativas
A) B
B) C
C) D
D) E
Respuesta
B)
Al unir los vértices del pentágono con el centro de la circunferencia donde está inscrito se forman 5 triángulos congruentes, tal como se muestra en la figura:
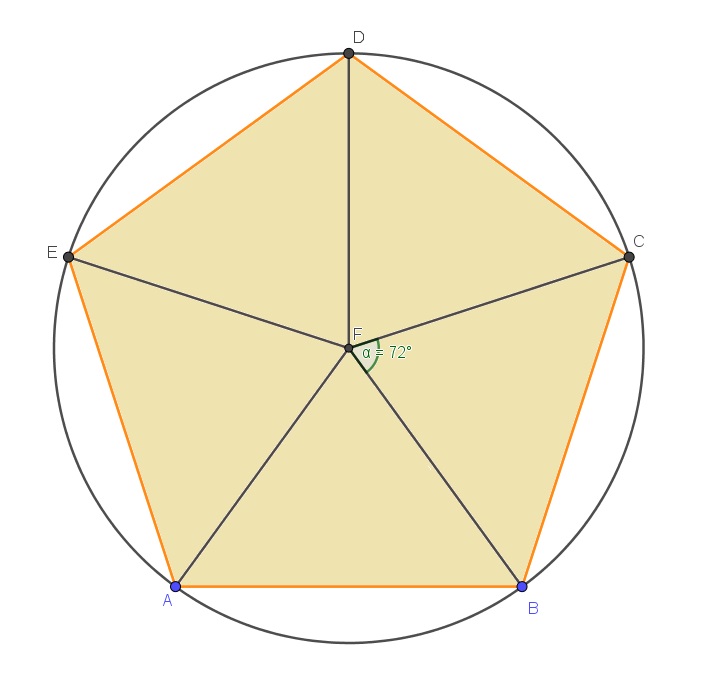
La medida de cada ángulo del centro es de 72$^{\circ}$, ya que la suma de los 5 ángulos debe ser 360$^{\circ}$. Al rotar el pentágono en 2$\cdot$ 72$^{\circ}$ = 144$^{\circ}$ en sentido antihorario en torno a F, el vértice A quedará en la posición donde se encontraba el vértice C inicialmente.
Movimientos geométricos
Enunciado
Observa la siguiente imagen.

La figura denotada con F´ se obtuvo al aplicar a la figura F una:
I. rotación en 180$^{\circ}$ con centro en el origen.
II. simetría central respecto al origen.
III. simetría axial respecto a la recta y = -x.
¿Cuál(es) de las afirmaciones es (son) verdadera(s)?
Alternativas
A) Solo I
B) Solo II
C) Solo I y II
D) Solo I y III
Respuesta
C
Analicemos cada una de las afirmaciones:
- al rotar F en 180$^{\circ}$, efectivamente se obtiene la figura F´.
- al realizar una simetría central respecto al origen, también es posible obtener F´. La distancia que hay entre cada punto de F y el origen es la misma que hay entre cada punto correspondiente de F´ y el origen. Esto, haciendo la correspondencia entre cada uno de los puntos de la figura.
- al realizarle una simetría axial a F respecto a la recta y = -x no es posible obtener F´ (la punta de la flecha estaría en el otro extremo).
Por lo tanto, las afirmaciones correctas son solo I y II.
Traslación por vectores
Enunciado
Considere los vectores $\vec{a}$ = (4, -2) y $\vec{b}$ = (-3, 4) como los que se observan en la siguiente figura:
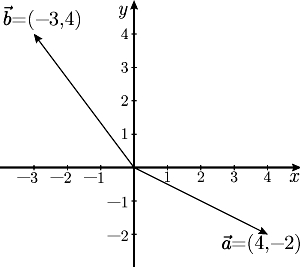
¿Cuál(es) de las siguientes afirmaciones es(son) verdadera(s)?
I) $\vec{a}$ - $\vec{b}$ = (7, 6)
II) 3$\vec{a}$ + $2\vec{b}$ = (6, 2)
III) -4$\vec{b}$ = (12, -16)
Alternativas
A) Solo I
B) Solo III
C) Solo I y II
D) Solo II y III
Respuesta
D
Note que $\vec{a}$ = (4, -2) y $\vec{b}$ = (-3, 4) por lo tanto:
$\vec{a} - \vec{b}$ = (4, -2) - (-3, 4) = (4 - (-3), -2 -4) = (7, -6) $\neq$ (7, 6)
3 $\vec{a} + 2 \vec{b}$ = 3$\cdot$(4 ,-2) + 2(-3, 4) = (12, -6) + (-6, 8) = (12 + (-6), -6 + 8) = (6, 2)
-4 $\vec{b}$ = -4$\cdot$(-3, 4) = (12, -16)
Recta
Enunciado
Al punto (-2,2) se le realiza una reflexión en torno a la recta: y = -x + 2, tal como lo muestra la imagen adjunta. ¿Cuál es el punto resultante?
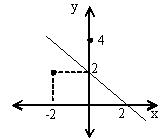
Alternativas
A) (2, -2)
B) (2, 0)
C) (0, 0)
D) (0, 4)
Respuesta
D)
Veamos que la recta y = -x + 2 posee:
- corte con eje y = 2.
- pendiente = -1.
Recordemos que una reflexión en torno a una recta debe poseer la misma distancia perpendicular; por lo tanto, el punto que cumple con lo solicitado es (0,4):
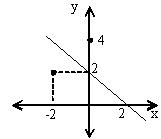
Traslaciones
Enunciado
Al trasladar el triángulo de vértices $A(-2,4), B(2,1)$ y $C(4,3)$ según el vector de traslación $(4,1)$, el vértice homólogo de $B$ es:
Alternativas
A) $(2,4)$
B) $(6,2)$
C) $(8,4)$
D) $(3,5)$
Respuesta
B)
Trasladando el punto $B$ obtenemos:
$(2,1) + (4,1) = (6,2)$
Centro de rotación
Enunciado
El triángulo PQT puede ser rotado de modo que quede encima del triángulo SQR.
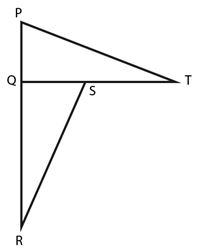 |
Para que ello ocurra, ¿cuál punto sería el centro de rotación?
Alternativas
A) P
B) Q
C) R
D) S
Respuesta
B) Q
Punto de rotación
Enunciado
El rectángulo PQRS puede ser rotado (girado) hasta coincidir con el rectángulo UVST.
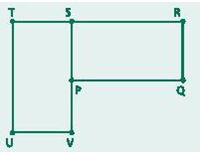 |
Para ello, ¿qué punto debe ser el centro de rotación?
Alternativas
A) Punto P
B) Punto R
C) Punto S
D) Punto T
Respuesta
C) Punto S
Reflexión
Enunciado
Escriba una X en uno de los cuadrados de abajo, de tal manera que si la tira de papel es doblada donde lo indica la línea, el cuadrado con la X que usted marque cubra al cuadrado sombreado.
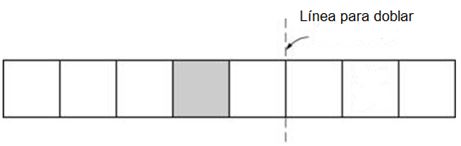 |
Respuesta
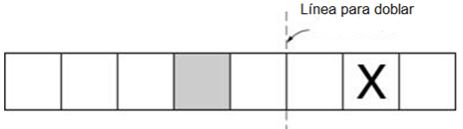 |
Rotación de medio giro
Enunciado
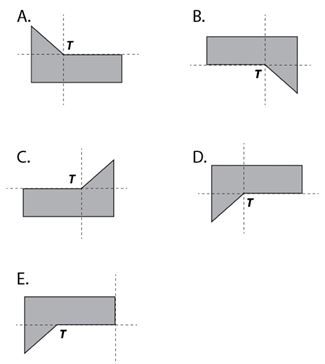
A la figura sombreada se le aplica un medio giro sobre el punto T del plano.
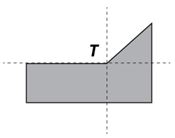 |
¿Cuál de las siguientes opciones muestra el resultado del medio giro?
Alternativas
 |
Respuesta
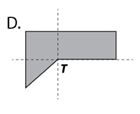 |