Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA07 OA 11
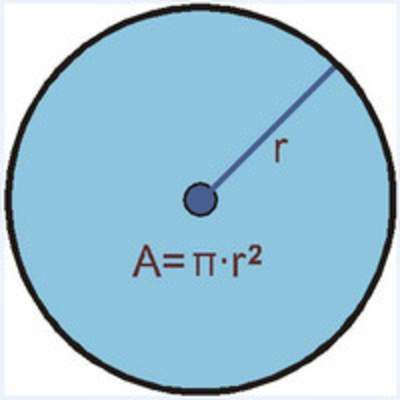
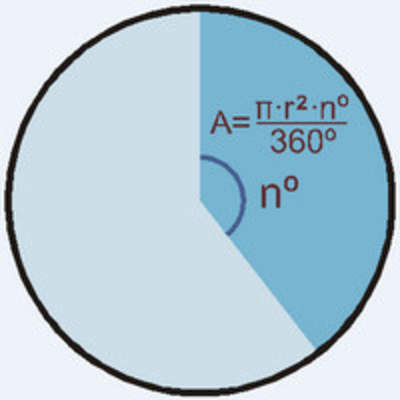
Mostrar que comprenden el círculo:
- Describiendo las relaciones entre el radio, el diámetro y el perímetro del círculo.
- Estimando de manera intuitiva el perímetro y el área de un círculo.
- Aplicando las aproximaciones del perímetro y del área en la resolución de problemas.
- Geométricos de otras asignaturas y de la vida diaria.
- Identificándolo como lugar geométrico.
Clasificaciones
Textos Escolares oficiales 2023
Actividades de apoyo pedagógico
Material didáctico
Lecciones: clases completas
Evaluaciones del programa
Indicadores
Indicadores Unidad 3
- Identifican la línea del ecuador, paralelos y meridianos en modelos esféricos.
- Miden el diámetro y el perímetro de objetos redondos, como vasos con forma cilíndrica, latas, corchos, etc.
- Calculan el cociente entre el perímetro y el diámetro de una"pi" circunferencia y comparar el resultado con.
- Aplican la fórmula P = d t pi en ejercicios rutinarios y no rutinarios, para resolver problemas que involucran perímetros de círculos, como ecuador, paralelos y meridianos.
- Estiman el área del círculo entre 2r2 y 4r2, descubriendo que también resulta el mismo valor aproximado de a ≈ r 2 t 3.
- Aplican la fórmula A = r2 t pi (con pi ≈3,14) en ejercicios rutinarios y en la solución de problemas que involucran áreas de círculos.
- Resuelven problema de la vida diaria que implican el cálculo de área de un círculo; por ejemplo: los cultivos en círculos para el ahorro de agua.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
El ojo de Londres
Enunciado
En Londres, a orillas del río Támesis está ubicada una rueda gigante denominada el Ojo de Londres (London Eye).
Véase la fotografía y el gráfico que se muestran a continuación.
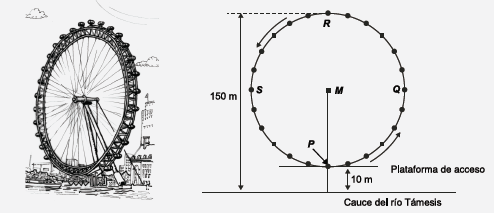
La rueda tiene un diámetro exterior de $140$ metros y su punto más alto se encuentra a $150$ metros sobre el cauce del río Támesis. Da vueltas en el sentido indicado por las flechas.
La rueda da vueltas a una velocidad constante. Se demora exactamente $40$ minutos en dar una vuelta completa.
Juan inicia su viaje en la rueda en el punto de acceso P.
¿Dónde estará Juan después de media hora?
Alternativas
A) En R.
B) Entre R y S.
C) En S.
D) Entre S y P.
Respuesta
C) En S.
Área en un círculo
Enunciado
A continuación, se muestra un círculo de radio $10$ centímetros.
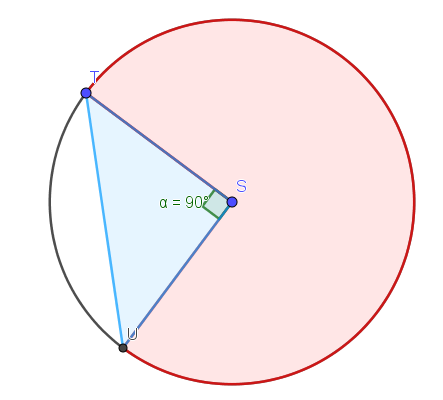
¿Cuántos centímetros cuadrados mide, aproximadamente, el área de la zona blanca de la figura? Recordar que $\pi \approx 3,14$
Alternativas
A) $50\:cm^{2}$
B) $214\:cm^{2}$
C) $70\:cm^{2}$
D) $28,5\:cm^{2}$
Respuesta
D)
El área del círculo completo es:
$\pi\cdot r^{2}=3,14\cdot10^{2}=3,14\cdot 100=314$
El sector blanco se encuentra en un cuarto de círculo.
El área del triángulo es:
$\dfrac{b\cdot h}{2}=\dfrac{10\cdot 10}{2}=50$
El área del cuarto de círculo es:
$\dfrac{100\cdot 3,14}{4} =78,5$
Entonces el área de la zona blanca es:
$78,5 - 50= 28,5$
Banco de Preguntas [Banco de preguntas-MA7 OA11-1048575] Matemática 7
Enunciado
En una casa se tienen vasos cuya área basal es de $60$ $cm^2$. La familia quiere comprar posavasos circulares para los vasos. El posavasos debe ser de área mayor que la de la base del vaso. ¿Cuál(es) de las siguientes opciones les sirven para sus vasos? (Considera $\pi\approx 3$).
I. Posavasos de diámetro $8$ $cm$.
II. Posavasos de diámetro $14$ $cm$.
III. Posavasos de radio $5$ $cm$.
Alternativas
A) Solo II
B) Solo I y II
C) Solo II y III
D) I II y III
Respuesta
C) Solo II y III
El caso I implica que el área del posavasos es aproximadamente $48$ $cm^2$ ya que si el diámetro es de $8$ $cm$ entonces su radio es de $4$ $cm$. El área se calcula elevando a $2$ la medida del radio y luego multiplicando dicho resultado por $\pi$ . Es decir: $4^2\cdot 3 = 48$ esto es menor que $60$ por lo que ese posavasos no les serviría.
El área del posavasos del caso II es: $7^2\cdot 3 = 147$ esto es mayor que $60$ por lo que el posavasos sí serviría.
El área del posavasos del caso III es $ 5^2\cdot 3 = 75$ esto es mayor que $60$ por lo que este posavasos sí le serviría.
El ojo de Londres
Enunciado
En Londres, a orillas del río Támesis, está ubicada una rueda gigante denominada el Ojo de Londres (London Eye), la que se ilustra en la siguiente imagen.
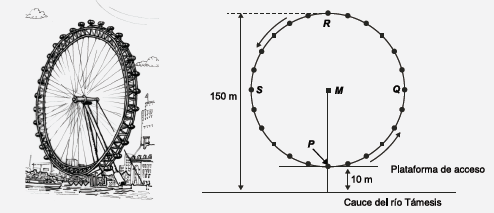
La rueda tiene un diámetro exterior de $140$ metros y su punto más alto se encuentra a $150$ metros sobre el cauce del río.
La letra M de la imagen señala el centro de la rueda.
¿A cuántos metros (m) sobre el cauce del río Támesis se encuentra el punto M?
Respuesta: ________ m
Respuesta
80
Lugar geométrico
Enunciado
Lee la siguiente definición:
"Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro".
¿A qué concepto corresponde la definición anterior?
Alternativas
A) Esfera.
B) Círculo.
C) Circunferencia.
D) Decágono regular.
Respuesta
C)
Definción de circunferencia:
- Es el lugar geométrico de los puntos del plano que distan una distancia fija llamada radio de un punto fijo llamado centro.
Problema con rotonda 2
Enunciado
Observa la siguiente rotonda:
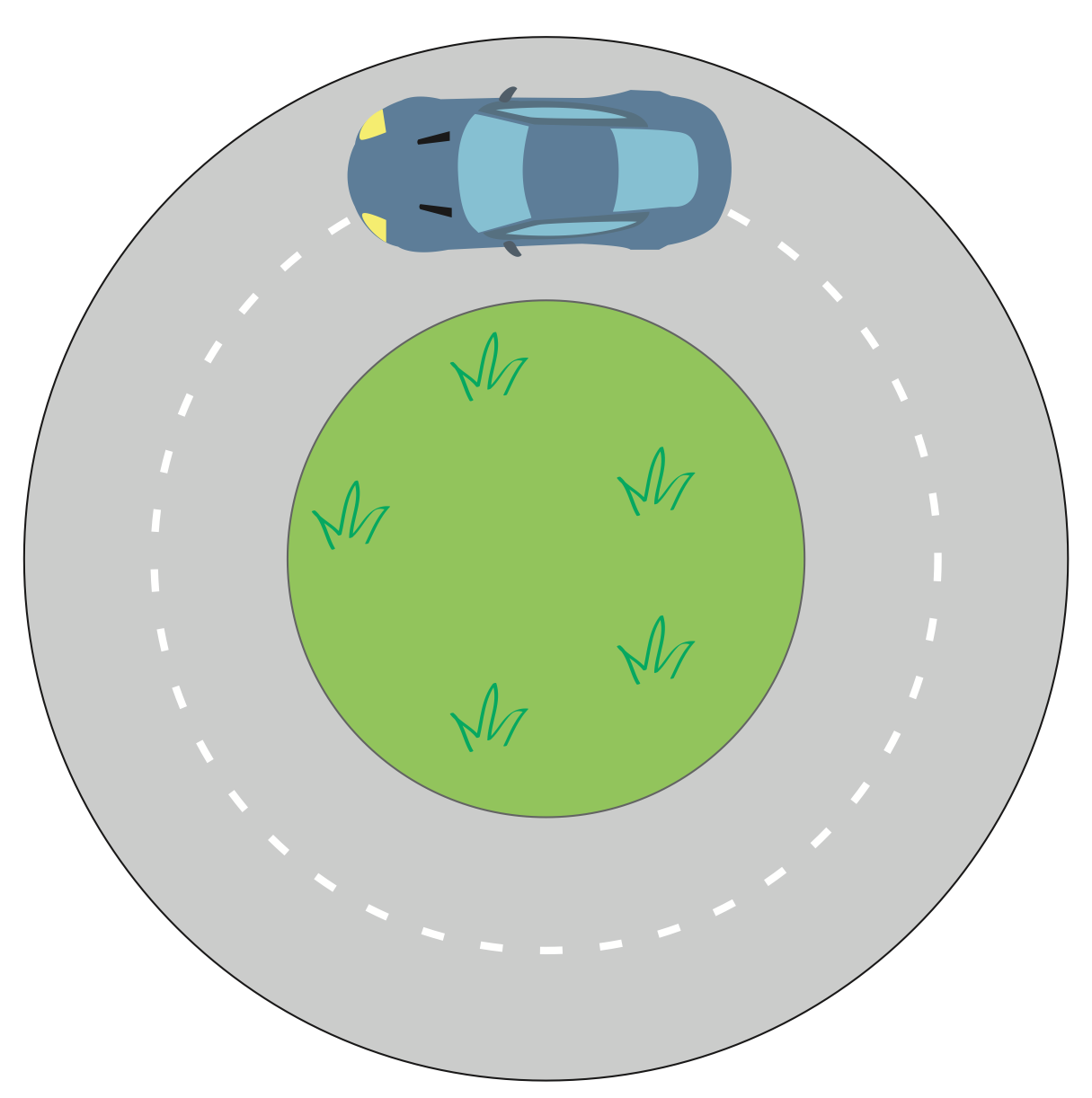
Sí un vehículo circula por la rotonda manteniéndose siempre a una distancia de 5 m del centro de ésta, ¿cuántos metros recorrería al dar una vuelta completa? Considere $\pi$ = 3.
Alternativas
A) 15 m
B) 30 m
C) 35 m
D) 75 m
Respuesta
B)
Es posible solucionar el problema a partir del cálculo del perímetro de la circunferencia. Sabemos que el perímetro se calcula como:
Perímetro $= 2 \pi r = 2 \times 3 \times 5 = 30 m$
RELOJ CIRCULAR
Enunciado
La imagen muestra un reloj circular de pared:
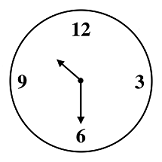
El reloj tiene un diámetro de 30 cm.
Considerando una aproximación de $\pi$ igual a 3, ¿cuál es el área de la superficie que ocupa el reloj?
Alternativas
A) $\ 80$ cm$^2$
B) $180$ cm$^2$
C) $675$ cm$^2$
D) $270$ cm$^2$
Respuesta
C)
El área de un círculo es $A=\pi \cdot r^2$
El diámetro del reloj es 30 cm, por lo tanto el radio es 15 cm.
Entonces, el área del círculo del reloj es:
$A=\pi \cdot r^2$
$A=3 \cdot 15^2$
$A=\pi \cdot r^2$
$A=3 \cdot 225$
$A=675$
Área de una rotonda
Enunciado
El diámetro de una rotonda es igual a $20$ $m$. ¿Cuál es la medida de su área? Considere $\pi =3$.
Alternativas
A) $60$ $m^2$
B) $120$ $m^2$
C) $300$ $m^2$
D) $1\:200$ $m^2$
Respuesta
C)
Si el diámetro de la rotonda es igual a $20$ $m$ su radio mide $10$ $m$.
Calculemos su área:
$A= \pi r^2$
$A=3 · 10^2$
$A=300$
El área de la rotonda es igual a $300$ $m^2$.
Áreas de círculos
Enunciado
¿Cuál es la mitad del área de un círculo de diámetro $20$ cm? (Considere $\pi =3,14$)
Alternativas
A) $157$ $cm^2$
B) $314$ $cm^2$
C) $628$ $cm^2$
D) $1\:256$ $cm^2$
Respuesta
A)
El área del círculo está dada por la fórmula $\pi \cdot r^{2}$ donde $r$ corresponde a la medida del radio. Es decir el área del círculo que menciona el enunciado es:
$$\pi \cdot 10^2=3,14 \cdot 100 = 314$$
El enunciado pregunta por la MITAD del área es decir $314:2=157$.
Por lo tanto la mitad del área del círculo es $157$ cm$^{2}$.
Áreas de círculos 2
Enunciado
Al posicionar un cartón circular bajo una luz, proyecta una sombra cuya área es el doble del área del cartón. Si el cartón tiene un radio de $5$ $cm$, ¿cuál es el área de la sombra que proyecta? (Considere $\pi =3$).
Alternativas
A) $10$ $cm^2$
B) $37,5$ $cm^2$
C) $75$ $cm^2$
D) $150$ $cm^2$
Respuesta
D)
El área del cartón es:
$$\pi \times r^2=3 \times (5 \ cm)^2=3 \times 25 \ cm^2=75 \ cm^2$$
Considerando que la sombra proyectada tiene el doble de área que el cartón entonces el área de la sombra es:
$$2 \times 75 \ cm^2=150 \ cm^2$$
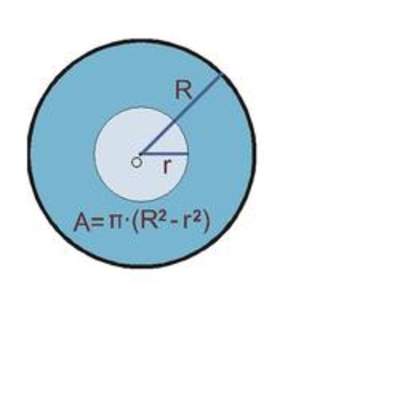
Círculos concéntricos
Enunciado
Se tienen dos círculos concéntricos con centro O y diámetros 8 y 12 cm respectivamente. ¿Cuál es la superficie achurada de la figura? (Use $ \pi = 3 $ ).

Alternativas
A) $6\;cm^2$
B) $240\;cm^2$
C) $156\;cm^2$
D) $60\;cm^2$
Respuesta
D) $60\;cm^2$
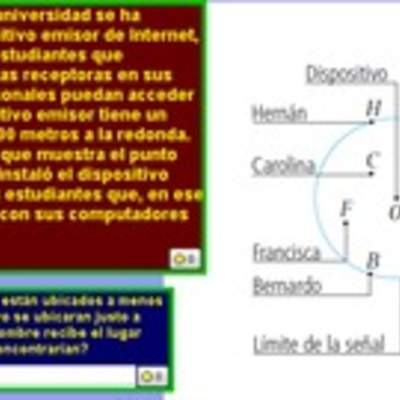
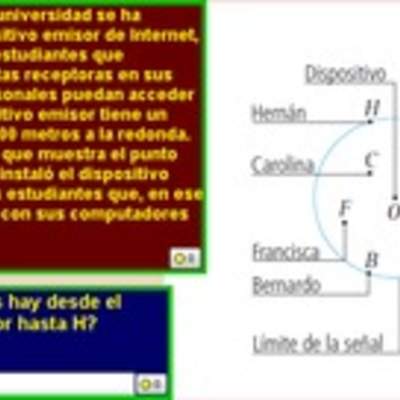
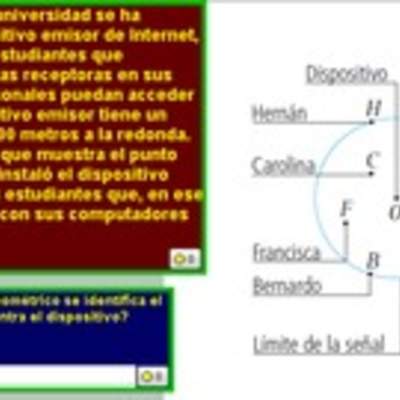
Cobertura de una antena
Enunciado
Una antena de celular tiene cobertura para una superficie circular de 588 $km^2$. ¿A qué distancia, como máximo, puede estar una persona para que su teléfono celular tenga cobertura? (Considere $\pi = 3$).
Alternativas
A) 14 km
B) 12 km
C) 18 km
D) 196 km
Respuesta
A
Contando círculos
Enunciado
En una pizarra rectangular de 120 cm de largo y 80 cm de ancho se dibujan círculos de radio 10 cm. ¿Cuántos círculos se podrán dibujar como máximo, sin superponer un círculo sobre otro?
Alternativas
A) 96 círculos.
B) 32 círculos.
C) 24 círculos.
D) 10 círculos.
Respuesta
C
Mezclando figuras
Enunciado
Se construye un cuadrado de 10 cm de radio. En el interior, se construyen dos cuartos de círculos, uno con radio de igual medida que el lado del cuadrado y el otro con radio cuya medida es la mitad del lado del cuadrado, tal como lo muestra la figura:

De acuerdo a la figura, ¿cuánto mide la superficie achurada? (Use $\pi = 3$ )
Alternativas
A) $56,25\;cm^2$
B) $30\;cm^2$
C) $25\;cm^2$
D) $225\;cm^2$
Respuesta
A)
Perímetro de circunferencias
Enunciado
El radio de una rueda mide 25 cm. Se puso la rueda en el suelo y se la hizo rodar hacia adelante cuatro vueltas completas. ¿Qué distancia recorrió la rueda? (Use $ \pi = 3 $ )
Alternativas
A) 600 cm
B) 150 cm
C) 300 cm
D) 200 cm
Respuesta
A
Pintando círculos
Enunciado
En una pizarra rectangular de 120 cm de largo y 80 cm de ancho se dibujan 24 círculos de radio 10 cm, sin superponer uno sobre otro. Se pintan todos los círculos de rojo, ¿qué superficie de la pizarra queda sin pintar? (Use $ \pi = 3 $ )
Alternativas
A) $ 5\:280\;cm^2 $
B) $ 8\:160\;cm^2 $
C) $ 7\:200\;cm^2 $
D) $ 2\:400\;cm^2 $
Respuesta
D)
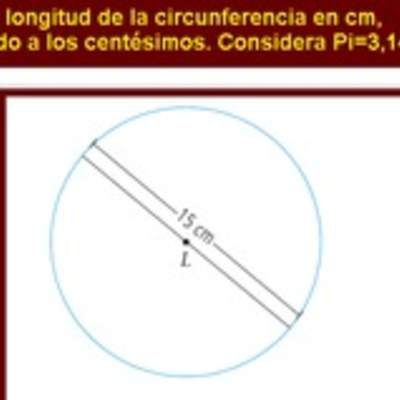
Problema de cálculo de perímetro de circunferencia.
Enunciado
La insignia de un colegio está confeccionada en base a un rectángulo. A sus puntas se le ha quitado un cuarto de circunferencia, tal como se muestra en el dibujo.
 |
Para el próximo año, se ha decidido colocar un hilo dorado por todo el contorno de la insignia. Para ello, ¿cuántos cm de hilo dorado se necesitan por insignia?
Alternativas
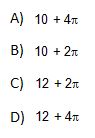 |
Respuesta
|
|
Pelotas de tenis
Enunciado:
Tres pelotas de tenis deben ser puestas una encima de la otra dentro de un tarro cilíndrico. El radio de cada pelota es de 3 centímetros. ¿Cuántos centímetros debería medir como mínimo el alto del tarro para que quepan las tres pelotas?
Respuesta:______________
| Explique por qué eligió esa altura. Su explicación debe incluir un diagrama: |
Respuesta:
18 centímetros.
Cada pelota tiene un diámetro de 6 centímetros (2 veces el radio de 3) y 3 pelotas x 6 centímetros cada una = 18 centímetros.
(La explicación puede consistir en una figura o en un texto que demuestre una comprensión visual de la pregunta).
Perímetro de una figura
Enunciado
En un lado de un cuadrado de 2 cm de lado se recortó un semicírculo que tiene como diámetro el lado del cuadrado. Luego, el semicírculo se agregó en el lado opuesto del cuadrado, como se muestra en la siguiente figura.
¿Cuánto mide el perímetro de la figura que se obtuvo?