Priorización 2023-2025: Aprendizajes Basales
CN2M OA 09
Analizar, sobre la base de la experimentación, el movimiento rectilíneo uniforme y acelerado de un objeto respecto de un sistema de referencia espacio-temporal, considerando variables como la posición, la velocidad y la aceleración en situaciones cotidianas.
Textos Escolares oficiales 2023
Física 1° y 2° Medio, Ediciones Malva, Guía didáctica del docente Tomo 3
Física 1º y 2° Medio, Ediciones Malva, Guía didáctica del docente Tomo 4
Actividades de apoyo pedagógico
Material didáctico
Lecciones: clases completas
Indicadores
Indicadores unidad 1
- Demuestran, con experimentos sencillos, por qué es necesario el uso de sistemas de referencia y de coordenadas en la descripción del movimiento de un objeto.
- Utilizan las fórmulas de adición de velocidades de Galileo en situaciones simples y cotidianas, como la de vehículos que se mueven unidimensionalmente.
- Explican conceptos de cinemática, como tiempo transcurrido, posición, desplazamiento, distancia recorrida, velocidad media e instantánea y aceleración, entre otros, asociados al movimiento rectilíneo de un objeto.
- Identifican características de la cinemática del movimiento rectilíneo, en fenómenos naturales y en situaciones cotidianas, como ocurre con la luz y con vehículos, respectivamente, entre otros ejemplos.
- Analizan, con conceptos de cinemática y herramientas gráficas y analíticas, el movimiento rectilíneo de un objeto en situaciones cotidianas.
- Explican el concepto de aceleración de gravedad incluyendo su desarrollo histórico, y consideran su uso en situaciones de caída libre y lanzamientos verticales.
- Obtienen conclusiones, en relación con conceptos de cinemática, a partir de investigaciones experimentales sobre objetos con movimiento rectilíneo con aceleración constante (nula o no nula).
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Distancia
Enunciado
En una vereda rectilínea una niña se mueve a 0,5 m/s al encuentro de su mascota, la cual corre en sentido opuesto a 1,5 m/s. La separación inicial entre ambas es de 30 m. Entonces, el camino recorrido por la niña hasta encontrarse con su mascota es:
Alternativas
A) 7,5 m.
B) 10 m.
C) 15 m.
D) 20 m.
Movimiento Rectilíneo Uniforme Acelerado
Enunciado
¿En cuál de las siguientes situaciones se puede asegurar que un objeto describe un movimiento rectilíneo uniforme acelerado?
Alternativas
A) Cuando cambia uniformemente su sentido de movimiento.
B) Cuando se acerca al origen de un sistema de referencia.
C) Cuando se aleja constantemente de su posición inicial en linea recta.
D) Cuando cambia uniformemente su velocidad manteniendo una trayectoria recta.
Rapidez
Enunciado
Un tren se mueve, en una vía recta, en sentido norte-sur con una rapidez de 120 km/h respecto al suelo. A un lado de las vías del tren existe una carretera paralela por la cual viaja un bus, en el mismo sentido del tren, con una rapidez de 100 km/h respecto al suelo. Dentro de uno de los vagones del tren hay un niño que corre en sentido sur-norte, con una rapidez de 20 km/h respecto al vagón. ¿Cuál es la rapidez del niño con respecto al conductor del bus?
Alternativas
A) 0 km/h.
B) 20 km/h.
C) 40 km/h.
D) 100 km/h.
Sistema de Coordenadas
Enunciado
Un cuerpo que se mueve con velocidad constante. Si se cambia el sistema de coordenadas que se utiliza para describir este movimiento, se mantendrá inalterada:
I. La magnitud de su desplazamiento.
II. La distancia recorrida por él.
III. Su rapidez.
Es(son) correcta(s):
Alternativas
A) Solo I.
B) Solo I y II.
C) Solo I y III.
D) I, II y III.
Velocidad
Enunciado
Una partícula se mueve con velocidad constante de magnitud V distinta de cero, respecto a un observador O. La misma partícula se puede encontrar simultáneamente en reposo respecto a otro observaror P, solo si P:
Alternativas
A) Se mueve en reposo.
B) Se mueve en la misma trayectoria de la partícula.
C) Se mueve con igual rapidez que el observador O.
D) Se mueve con igual velocidad que el observador O.
Velocidad constante
Enunciado
Para que un objeto describa un movimiento rectilíneo uniforme es suficiente que su:
Alternativas
A) Trayectoria sea recta.
B) Rapidez sea constante.
C) Velocidad sea constante.
D) Desplazamiento sea recto.
Cinemática
Enunciado
Un automóvil es acelerado desde el reposo y recorre $54$ $[m]$ en $t$ $[s]$. Si la aceleración fue $3$ $[\frac{m}{s^2}]$, ¿cuál es el valor de $t$?
Alternativas
A) $3$ $[s]$
B) $5$ $[s]$
C) $6$ $[s]$
D) $9$ $[s]$
Cinemática
Enunciado
Un camión se mueve inicialmente a $6$ $[\frac{m}{s}]$ y luego acelera uniformemente hasta moverse a $10$ $[\frac{m}{s}]$, tras recorrer una distancia de $8$ $[m]$. Si se mueve rectilíneamente, ¿cuál fue la magnitud de la aceleración?
Alternativas
A) $4$ $[\frac{m}{s^2}]$
B) $8$ $[\frac{m}{s^2}]$
C) $16$ $[\frac{m}{s^2}]$
D) $32$ $[\frac{m}{s^2}]$
Movimiento y trayectoria
Enunciado
Un grupo de trabajadores de la construcción se encuentra en el quinto piso y desde el balcón, por accidente, a uno de ellos se le cae una piedra. A partir de lo anterior, ¿cuál de las siguientes opciones es correcta respecto a la trayectoria de la piedra que observa el trabajador directamente desde arriba en el balcón?
Alternativas
A) Linea curva
B) Linea recta
C) Un punto
D) Irregular con lineas rectas y curvas
Cinemática
Enunciado
Se determina que la luz tarda tan solo ${10}^{-7}$ segundos en atravesar una pared de vidrio, cuyo índice de refracción es $2$. De acuerdo con la información anterior, ¿cuál es el grosor de la pared?
Alternativas
A) $150$ $[m]$
B) $15$ $[m]$
C) $1,5$ $[m]$
D) $0,15$ $[m]$
Cinemática
Enunciado
Sobre una plataforma que se mueve con velocidad constante en la dirección del eje x se lanza una piedra verticalmente hacia arriba. La trayectoria de la piedra percibida por un observador que se encuentra en reposo en el exterior de la plataforma será:
Alternativas
A) 
B) 
C) 
D) 
Caída libre
Enunciado
Desde la azotea de un edificio un niño deja caer una moneda al piso. La moneda tarda $3$ segundos en llegar al suelo. Si aproximamos la aceleración de gravedad de la Tierra a $g = 10 \frac{m}{s^2}$ la altura desde la que cayó la moneda es:
Alternativas
A) $45$ metros.
B) $90$ metros.
C) $30$ metros.
D) $15$ metros.
Calcular velocidad
Enunciado
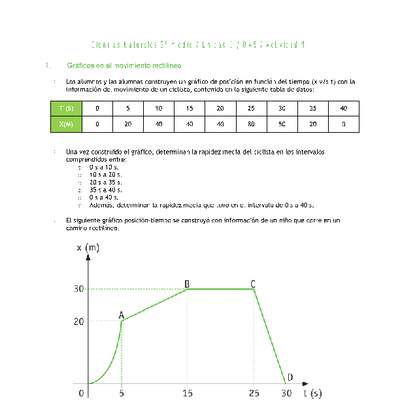
El gráfico muestra lo que ha avanzado un escarabajo que se mueve en línea recta.
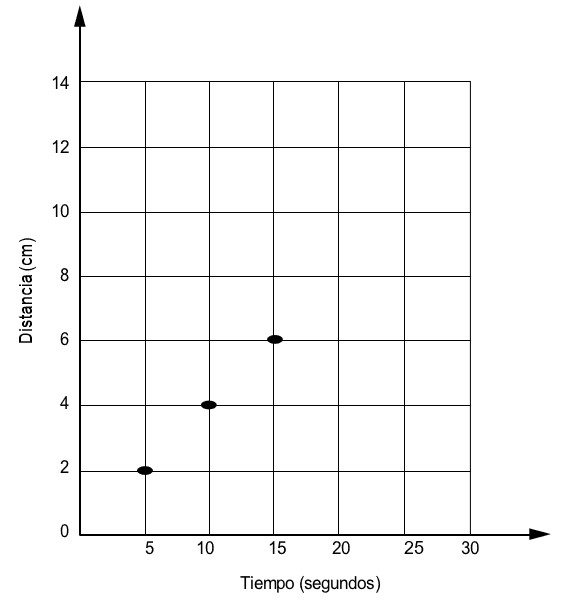
Si el escarabajo sigue avanzando a la misma velocidad, ¿cuánto tiempo demorará en recorrer 10 cm?
Alternativas
A) 4 segundos.
B) 6 segundos.
C) 20 segundos.
D) 25 segundos.
Cinemática
Enunciado
¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s) con respecto a un móvil que describe movimiento uniformemente retardado?
I. Posee aceleración negativa y constante.
II. El sentido de la velocidad es negativa en todo momento
III. El módulo de la velocidad disminuye de manera uniforme.
Alternativas
A) Solo I
B) Solo II
C) Solo I y III
D) Solo III
Velocidad de la luz
Enunciado
¿Cuál es la distancia que recorre la luz en 0,01 [s] viajando a 250.000 Km/s?
Alternativas
A) 250.000 [m]
B) 25.000 [m]
C) 2.500 [km]
D) 250 [m]
