Habilidades
Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA1M OA 10
Aplicar propiedades de semejanza y de proporcionalidad a modelos a escala y otras situaciones de la vida diaria y otras asignaturas.
Clasificaciones
Textos Escolares oficiales 2023

Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 1

Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 2
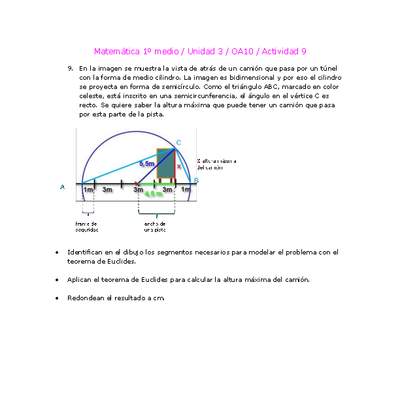
Actividades de apoyo pedagógico
Lecciones: clases completas
Indicadores
Indicadores unidad 3
- Comparan modelos de objetos reales con el original y mencionan las relaciones que existen entre ellos.
- Calculan, a partir de las medidas de un modelo, las medidas de un objeto real, y viceversa.
- Determinan la escala entre el modelo y la realidad.
- Determinan factores de aumento o de reducción en imágenes.
- Modelan situaciones reales, como determinar el tamaño de una plaza utilizando modelos a escala.
- Verifican pictóricamente el teorema de Euclides a partir de un triángulo rectángulo isósceles.
- Comprueban el teorema de Euclides mediante triángulos semejantes, dentro del triángulo rectángulo.
- Aplican el teorema de Euclides en problemas geométricos y de la vida cotidiana.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Propiedades de homotecia
Enunciado
La figura EFGH se obtiene al aplicar una homotecia de centro O y razón k a la figura ABCD:

Al respecto, ¿cuál(es) de las siguientes afirmaciones es (son) correcta(s)?
I. k $<$ 0
II. $\overrightarrow{OF}$ = k$\cdot \overrightarrow{OB}$
III. $\overrightarrow{OA}$ = k$\cdot\overrightarrow{OE}$
Alternativas
A) Solo I
B) Solo III
C) I, II y III
D) Solo I y II
Respuesta
D
Al aplicar una homotecia a una figura, lo que se hace es multiplicar la razón de homotecia y el vector que se define desde el centro de la homotecia a cada punto de la figura. En primer lugar, es necesario identificar la imagen de cada punto original: $E$ es la imagen de $A$, $H$ es la imagen de $D$, $G$ es la imagen de $C$ y $F$ es la imagen de $B$. Segun esto, se tiene:
$\overrightarrow{\mbox{OE}}$ = k$\cdot\overrightarrow{\mbox{OA}}$
$\overrightarrow{\mbox{OH}}$ = k$\cdot\overrightarrow{\mbox{OD}}$
$\overrightarrow{\mbox{OG}}$ = k$\cdot\overrightarrow{\mbox{OC}}$
$\overrightarrow{\mbox{OF}}$ = k$\cdot\overrightarrow{\mbox{OB}}$
Por otro lado, la figura homotética está rotada respecto de la figura original, por lo que la constante $k$ es negativa.
Se concluye que solo las afirmaciones I y II son ciertas.
Banco de Preguntas [Banco de preguntas-MA1M OA10-37664] Matemática 1M
Enunciado
En el siguiente plano el ancho de la calle Blaise Pascal es igual a 0,5 cm y su largo es igual a 10 cm. Si en la realidad el ancho mide 6 m y el largo mide 120 m, ¿cuál es la escala entre el modelo y la realidad?

Alternativas
A) 1 : 12
B) 1 : 20
C) 1 : 1 200
D) 1 : 24000
Respuesta
C
Primero transformemos las dimensiones reales de la calle a centímetros:
ancho$_{realidad}$ = 6 m = 600 cm
largo$_{realidad}$ = 120 m = 12 000 cm
Determinemos la escala entre el modelo y la realidad:
$\dfrac{ancho_{plano}}{ancho_{realidad}}=\dfrac{largo_{plano}}{largo_{realidad}} = \dfrac{0,5}{600}=\dfrac{10}{12 000}=\dfrac{10}{12 000}=\dfrac{1}{1 200}$
Por lo tanto, la escala entre el modelo y la realidad es 1 : 1 200.
Comparación de modelos
Enunciado
Si $\triangle ABC\cong \triangle DEF$; entonces, se puede afirmar que:
Alternativas
A) $\overline{AC}\cong \overline{DF}$
B) $\overline{AB}\cong \overline{FE}$
C) $\overline{AB}\cong \overline{FD}$
Respuesta
A
Si el $\triangle ABC \cong \triangle DEF$ se obtienen las siguientes relaciones de acuerdo a sus lados homólogos:
- $\overline{AB} \cong \overline{DE}$
- $\overline{AC} \cong \overline{DF}$
- $\overline{BB} \cong \overline{EF}$
De lo cual se concluye que $\overline{AC}\cong \overline{DF}$.