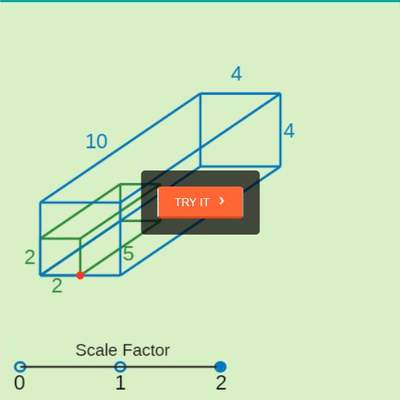
Habilidades
Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA1M OA 08
Mostrar que comprenden el concepto de homotecia:
- Relacionándola con la perspectiva, el funcionamiento de instrumentos ópticos y el ojo humano.
- Midiendo segmentos adecuados para determinar las propiedades de la homotecia.
- Aplicando propiedades de la homotecia en la construcción de objetos, de manera manual y/o con software educativo.
- Resolviendo problemas de la vida cotidiana y de otras asignaturas.
Clasificaciones
Textos Escolares oficiales 2023

Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 1

Matemática 1° medio, Santillana, Guía didáctica del docente Tomo 2
Actividades de apoyo pedagógico
Lecciones: clases completas
Evaluaciones del programa
Indicadores
Indicadores unidad 3
- Representan modelos de la homotecia de manera concreta (fuente de luz puntual, vela, ampolleta, lápiz, bloque, etc.).
- Reconocen las propiedades de la homotecia, como paralelismo, conservación del ángulo y conservación de razones.
- Conjeturan sobre el factor de la homotecia.
- Realizan homotecias en el plano, identificando el rayo óptico con el rayo geométrico.
- Realizan homotecias mediante el centro y el factor dado.
- Realizan homotecias mediante el centro y un par de imagen y preimagen dado.
- Aplican la homotecia en modelos ópticos, como la "cámara oscura", el ojo humano y fenómenos de la Tierra y el universo.
- Resuelven problemas de la vida cotidiana y de otras asignaturas.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Homotecia 1
Enunciado
Al triángulo $\Delta$ ABC se le aplicó una homotecia con centro en D, obteniéndose el triángulo $\Delta$ A´B´C´.
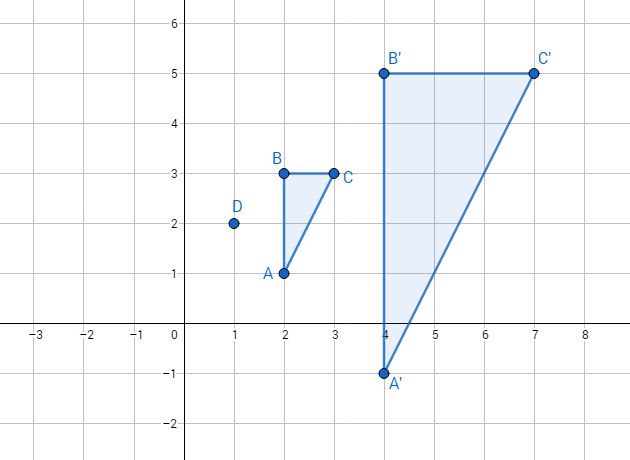
¿Cuál fue la razón de homotecia aplicada?
Alternativas
A) -2
B) 2
C) 3
D) -3
Respuesta
C)
La razón de homotecia sabemos que se puede determinar calculando el cociente entre el segmento homotético y el segmento original; es decir:
$\dfrac{\overline{DB'}}{\overline{DB}}$ = $\dfrac{3}{1}$
$\dfrac{\overline{DB'}}{\overline{DB}}$ =3
Por lo tanto, la razón de homotecia aplicada es igual a 3.
Banco de Preguntas [Banco de preguntas-MA1M OA08-23145] Matemática 1M
Enunciado
La figura EFGH se obtiene al aplicar una homotecia de centro O y razón k a la figura ABCD:

Al respecto, ¿cuál(es) de las siguientes afirmaciones es (son) correcta(s)?
I. k $<$ 0
II. $\overrightarrow{OF}$ = k$\cdot \overrightarrow{OB}$
III. $\overrightarrow{OA}$ = k$\cdot\overrightarrow{OE}$
Alternativas
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
Respuesta
D
Al aplicar una homotecia a una figura, lo que se hace es multiplicar la razón de homotecia y el vector que se define desde el centro de la homotecia a cada punto de la figura. En primer lugar, es necesario identificar la imagen de cada punto original: $E$ es la imagen de $A$, $H$ es la imagen de $D$, $G$ es la imagen de $C$ y $F$ es la imagen de $B$. Segun esto, se tiene:
$\overrightarrow{\mbox{OE}}$ = k$\cdot\overrightarrow{\mbox{OA}}$
$\overrightarrow{\mbox{OH}}$ = k$\cdot\overrightarrow{\mbox{OD}}$
$\overrightarrow{\mbox{OG}}$ = k$\cdot\overrightarrow{\mbox{OC}}$
$\overrightarrow{\mbox{OF}}$ = k$\cdot\overrightarrow{\mbox{OB}}$
Por otro lado, la figura homotética está rotada respecto de la figura original, por lo que la constante $k$ es negativa.
Se concluye que solo las afirmaciones I y II son ciertas.
Homotecia 2
Enunciado
En la siguiente imagen los cuadriláteros ABCD y PQRS son dos figuras homotéticas con centro en O.

Si sabe que $\overline{OA}\cong\overline{OP}$ $\overline{OB}\cong\overline{OQ}$ $\overline{OC}\cong\overline{OR}$ y $\overline{OD}\cong\overline{OS}$, ¿cuál es la razón de la homotecia?
Alternativas
A) -2
B) -1
C) 0
D) 2
Respuesta
B)
Veamos que estas dos figuras homotéticas tienen en común que distan una misma distancia del centro de la homotecia; además, están una a cada lado del centro. Esto quiere decir que es una homotecia inversa, por lo que la razón de homotecia es negativa. Además, como tienen la misma distancia desde el centro, la figura que se genera por homotecia no sufre ningún efecto de ampliación o disminución y, en consecuencia, su tamaño se mantiene. Por esto, la razón de homotecia, en este caso, es -1.
Homotecia
Enunciado
En la siguiente imagen la figura F2 se obtuvo aplicando una homotecia de centro E y factor $k$ a la figura F1.
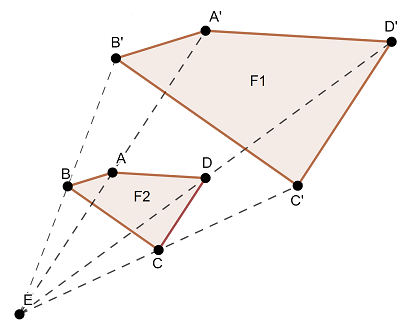
Si $\overline{EC}$ mide lo mismo que $\overline{CC´}$, ¿cuál es el factor k de la homotecia aplicada?
Alternativas
A) $- \dfrac{1}{2}$
B) $-2$
C) $\ \ \ 2$
D) $\ \ \dfrac{1}{2}$
Respuesta
D