Priorización 2023-2025: Aprendizajes Basales
MA07 OA 08
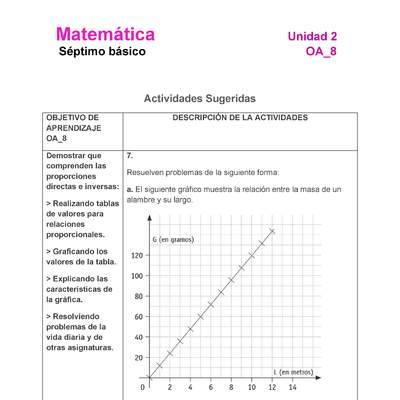
Mostrar que comprenden las proporciones directas e inversas:
- Realizando tablas de valores para relaciones proporcionales.
- Graficando los valores de la tabla.
- Explicando las características de la gráfica.
- Resolviendo problemas de la vida diaria y de otras asignaturas.
Textos Escolares oficiales 2023
Actividades de apoyo pedagógico
Identificar variables relacionadas en forma proporcional y no proporcional
Material didáctico
Lecciones: clases completas
Evaluaciones del programa
Indicadores
Indicadores Unidad 2
- Reconocen cambios en la vida cotidiana que se desarrollan en forma directamente proporcional.
- Completan y elaboran tablas de valores que pertenecen a proporcionalidades directas.
- Confeccionan gráficos que pertenecen a proporcionalidades directas.
- Reconocen cambios en la vida cotidiana que se desarrollan en forma inversamente proporcional.
- Explican la diferencia entre proporcionalidad directa e inversa.
- Reconocen la proporcionalidad directa e inversa en tablas de valores, gráficos y situaciones reales.
- Resuelven problemas mediante la proporcionalidad correspondiente.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Tasa de cambio
Enunciado
Mei-Ling de Singapur se preparaba para ir a Sudáfrica por 3 meses como estudiante de intercambio.
Ella necesitaba cambiar algunos dólares de Singapur (SGD) por rands sudafricanos (ZAR).
Mei-Ling se enteró que la tasa de cambio entre dólares de Singapur y rands sudafricanos era la siguiente:
1 SGD = 4,2 ZAR
Mei-Ling cambió 3 000 dólares de Singapur por rands sudafricanos a esta tasa de cambio.
¿Cuántos rands sudafricanos recibió Mei-Ling?
Tasa de cambio 2
Enunciado
Mei-Ling de Singapur fue de intercambio a Sudáfrica por 3 meses. Al regresar le quedan 3 900 rands sudafricanos (ZAR) y quiere cambiarlos por dólares de Singapur (SGD).
La tasa de cambio es:
1 SGD = 4,0 ZAR
¿Cuánto dinero en dólares de Singapur recibirá a cambio de los 3 900 ZAR?
Banco de Preguntas [Banco de preguntas-MA7 OA08-15572] Matemática 7
Enunciado
Un automóvil se mueve de forma rectilínea a velocidad constante de 20$\frac{m}{s}$. Después de 8 segundos su velocidad disminuye uniformemente hasta que se detiene. ¿Cuál de los siguientes gráficos representa mejor la situación descrita?
Alternativas
A) 
B) 
C) 
D) 
Proporcionalidad directa e inversa
Enunciado
¿Cuál de las siguientes magnitudes es una proporción directa?
Alternativas
A) El número de pintores y el tiempo que tardan en pintar una casa.
B) La rapidez con la que se recorre un camino y el tiempo en que se recorre.
C) El caudal de una llave y el tiempo que se demora en llenar un estanque.
D) El valor de un kilogramo de cierto producto y la cantidad final a pagar.
Banco de Preguntas [Banco de preguntas-MA7 OA08-28965] Matemática 7
Enunciado
¿Cuál de las siguientes variables están en una relación de proporcionalidad inversa?
Alternativas
A) El número de asistentes a una función de cine y el precio de la entrada.
B) El número de obreros y el tiempo que tardan en terminar una obra.
C) La estatura de una persona y su masa corporal.
D) La medida de los lados de un cuadrado y su perímetro.
Banco de Preguntas [Banco de preguntas-MA7 OA08-28968] Matemática 7
Enunciado
Alejandra disponía de $25$ litros de pintura para pintar su casa. Ella estima que, en promedio, ha gastado $2,5$ litros por hora. Si en total ha pintado durante $5,5$ horas, ¿cuántos litros de pintura le quedan?
Alternativas
A) $11,25$ litros.
B) $12,75$ litros.
C) $13,25$ litros.
D) $14,25$ litros.
Banco de Preguntas [Banco de preguntas-MA7 OA08-35730] Matemática 7
Enunciado
Una manguera demora $9$ minutos en llenar una piscina. ¿Cuántos minutos demorarán $3$ de estas mangueras en llenar la psicina?
Alternativas
A) $3$
B) $6$
C) $8$
D) $15$
Inversamente proporcional
Enunciado
¿En cuál(es) de las siguientes afirmaciones las dos variables presentan una relación inversamente proporcional?
I. La cantidad de pintura necesaria para pintar una superficie y la magnitud de la superficie que se desea pintar.
II. La cantidad de llaves que se usan para llenar un estanque y el tiempo que demoran en llenarlo.
III. El valor de la cuota que debe pagar cada persona y el número de personas se repartirán equitativamente el total a pagar.
Alternativas
A) Solo I
B) Solo II
C) Solo III
D) Solo II y III
Completando la tabla
Enunciado
¿Cúal es el valor de a y b para que X e Y sean magnitudes inversamente proporcionales?
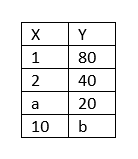
Respuesta:
a = ____
b = _____
Comprando pan
Enunciado
La señora Juanita compra en una panadería 3 kg. de pan y paga por ellos $ 3 450 en total. Al día siguiente, la señora Juanita comprará en la misma panadería 2 kg. de pan, ¿cuánto deberá pagar?
Alternativas
A) $ 1 150
B) $ 5 750
C) $ 5 175
D) $ 2 300
Descubriendo la proporción inversa
Enunciado
¿En cuál de las siguientes situaciones se establece una proporcionalidad inversa?
Alternativas
A) La cantidad de maquinas iguales que realizan un trabajo y el tiempo que demoran en realizarlo.
B) La población final de bacterias después de reproducirse y la cantidad inicial de bacterias.
C) El valor pagado al comprar una cantidad de kg de tomates y el precio de 1 Kg de tomates.
D) La cantidad de personas que ingresan a la Universidad a estudiar una carrera y el tiempo en que demoran en titularse.
Un pequeño viaje: calculando velocidades promedio
Enunciado
La distancia entre Rancagua y Concepción es, aproximadamente, de $420$ km. Un automóvil realiza este recorrido sin detenciones y demora $210$ minutos viajando a una rapidez promedio de $120$ $\frac {km}{h}$. Un bus hace el mismo recorrido sin detenciones y se demora $252$ minutos.
¿A qué rapidez promedio se desplazó el bus?
Alternativas
A) $144$ $\frac {km}{h}$
B) $100$ $\frac {km}{h}$
C) $78$ $\frac {km}{h}$
D) $162$ $\frac {km}{h}$
Problema de proporción
Enunciado
Sofía tiene una fotografía de 9 cm por 12 cm y quiere ampliarla. ¿Cuál de las siguientes medidas corresponde a una ampliación proporcional de la fotografía?
Alternativas
A) 11 cm por 14 cm.
B) 12 cm por 16 cm.
C) 14 cm por 17 cm.
D) 18 cm por 6 cm.
DESAFÍO :Problema de proporción 2
Enunciado:
Para embaldosar un piso se usan 2 tipos de baldosas cuadradas que tienen igual tamaño, pero distinto diseño. Cada tipo de baldosa está formada por 4 cuadrados pequeños, como se muestra en la siguiente imagen.
El diseño del piso require que por cada baldosa B se usen dos baldosas A.
A) Si para hacer el diseño se utilizan $60$ "Baldosas B", ¿cuántas baldosas se necesitan en total?
Respuesta: ___________________________________________________________________
B) ¿Qué parte del piso embaldosado quedará formado por cuadrados pequeños negros?
Respuesta: ___________________________________________________________________
Problema de proporción 4
Enunciado
Un auto tiene un estanque de bencina con una capacidad de 45 litros. El auto consume 8,5 litros de bencina por cada 100 km recorridos. Se hizo un viaje de 350 km con el estanque de bencina lleno. ¿Cuánta bencina quedó en el estanque al final del viaje?
Alternativas
A) 15, 25 litros
B) 16, 25 litros
C) 24, 75 litros
D) 29,75 litros
Desafío: Problema de proporcionalidad
Enunciado
Tres hermanos - Roberto, Daniel y Marcos- necesitan repartir $ \$45\ 000$ pesos para comprar regalos para sus hijos. Deciden repartir el dinero en proporción con el número de hijos que tiene cada uno. Roberto tiene $2$ hijos, Daniel tiene $3$ hijos y Marcos tiene $4$ hijos. ¿Cuánto dinero recibirá Marcos?
Alternativas
A) $ \$ \ 5\ 000$
B) $ \$10\ 000$
C) $ \$15\ 000$
D) $ \$20\ 000$
Problema de proporcionalidad 10
Enunciado
Un auto tiene un estanque con capacidad para 35 litros de combustible. El auto consume 7,5 litros de combustible por cada 100 km de recorrido. Si se inicia un viaje de 250 km con el estanque lleno de combustible, ¿cuánto queda en el estanque al final del viaje?
Alternativas
A) 16,25 litros
B) 17,65 litros
C) 18,75 litros
D) 23,75 litros
Problema de proporcionalidad 11
Enunciado
El corazón de una persona late 72 veces por minuto. A este ritmo, ¿cuántas veces late en una hora, aproximadamente?
Alternativas
A) 430 000
B) 4 200
C) 4 300
D) 430
Problema de proporcionalidad 12
Enunciado
Tres quintas partes de un curso son niñas. Si al curso se agregan 5 niñas y 5 niños, ¿cuál de estas afirmaciones respecto del curso es verdadera?
Alternativas
A) Hay más niñas que niños.
B) Hay más niños que niñas.
C) Hay igual número de niñas y niños.
D) Con la información entregada no se puede afirmar si hay más niñas o niños.
Problema de proporcionalidad 13
Enunciado
Si hay 300 calorías en 100 g de un alimento determinado, ¿cuántas calorías hay en una porción de 30 g de ese alimento?
Alternativas
A) 10
B) 90
C) 900
D) 1 000
Problema de proporcionalidad 2
Enunciado
En la siguiente figura, el segmento PQ mide 60 cm y las medidas de los segmentos PR y RQ están en razón 2:3.
 |
¿Cuánto mide el segmento RQ?
Alternativas
A) 40 cm
B) 36 cm
C) 24 cm
D) 20 cm
Problema de proporcionalidad 3
Enunciado
Paula y Danilo decidieron aportar una cantidad proporcional de sus ahorros para comprar un disco que cuesta 4 000 pesos. Si Paula tiene ahorrados 6 000 pesos y Danilo 10 000 pesos, ¿cuánto debe aportar Paula para comprar el disco?
Alternativas
A) 1 000 pesos.
B) 1 500 pesos.
C) 1 600 pesos.
D) 2 400 pesos.
Problema de proporcionalidad 4
Enunciado
Los tres octavos básicos están planificando un viaje para el cual deben reunir $180 000. Algunos piensan que cada curso debe aportar un tercio del dinero. Otros piensan que el aporte de cada curso debe ser proporcional a la cantidad de estudiantes.
La siguiente tabla muestra la cantidad de estudiantes por curso.
| Curso | Cantidad de Estudiantes |
| 8°A | 35 |
| 8°B | 45 |
| 8°C | 40 |
El presidente del 8º C afirma: "Con cualquiera de las dos alternativas mi curso debe aportar con un tercio del dinero".
¿Estás de acuerdo con la afirmación del presidente del 8º C?
Respuesta:
Sí ____
No ____
| Fundamenta tu respuesta y muestra en el siguiente espacio los cálculos realizados. . |
Problema de proporcionalidad 9
Enunciado
Una máquina usa 2,4 litros de gasolina por cada 30 horas de funcionamiento. ¿Cuántos litros de gasolina usará la máquina en 100 horas?
Alternativas
A) 7,2
B) 8,0
C) 8,4
D) 9,6
Proporcionalidad como igualdad de razones (I)
Enunciado
Observa la siguiente expresión:
El valor de n es igual a:
Alternativas
A) 3
B) 7
C) 36
D) 63
Proporcionalidad como igualdad de razones 2
Enunciado
Si la razón entre 7 y 13 es igual a la razón entre x y 52, ¿cuál es el valor de x?
Alternativas
A) 7
B) 13
C) 28
D) 46
Proporcionalidad como igualdad de razones 3
Enunciado
La tabla muestra algunos valores de x e y, donde x es proporcional a y.
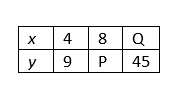
¿Cuáles son los valores de P y Q?
Alternativas
A) P = 5 y Q = 32
B) P = 13 y Q = 40
C) P = 18 y Q = 20
D) P = 27 y Q = 12
