Grupo: Título del recurso
Priorización 2023-2025: Aprendizajes Basales
MA05 OA 22
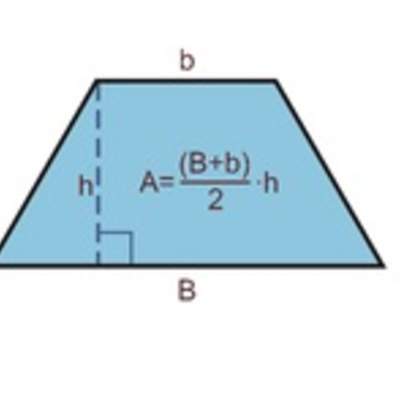
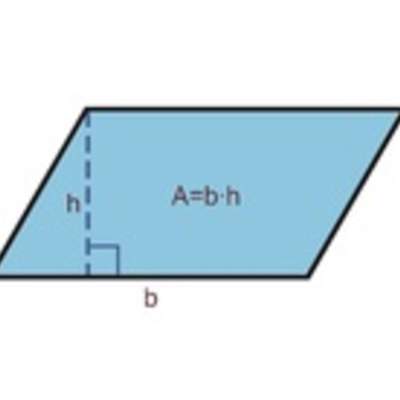
Calcular áreas de triángulos, de paralelogramos y de trapecios, y estimar áreas de figuras irregulares aplicando las siguientes estrategias:
- conteo de cuadrículas
- comparación con el área de un rectángulo
- completar figuras por traslación.
Clasificaciones
Textos Escolares oficiales 2023

Sumo Primero 5° Básico, Texto del Estudiante Tomo 1. Edición 2024

Sumo Primero 5° Básico, Texto del Estudiante Tomo 2. Edición 2024

Sumo Primero 5° Básico, Mineduc, Guía Didáctica Docente Tomo 1. Edición 2024

Matemática 5º básico, Santillana, Guía didáctica del docente Tomo 1

Matemática 5º básico, Santillana, Guía didáctica del docente Tomo 2

Sumo Primero 5° Básico, Mineduc, Guía Didáctica Docente Tomo 2. Edición 2024
Material didáctico
Indicadores
Indicadores Unidad 2
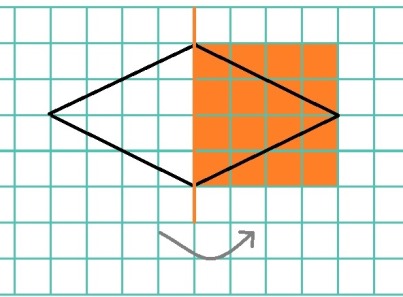
- Forman figuras en el plano, trasladando figuras. Por ejemplo: trasladan dos triángulos para unirlos a un rectángulo y forman un trapecio.
- Forman figuras del plano a partir de reflexiones. Por ejemplo: reflejan un triángulo equilátero respecto de uno de sus lados para formar un rombo.
- Transforman figuras del plano en otras de igual área, aplicando transformaciones isométricas. Por ejemplo: aplican traslaciones para transformar paralelogramos en rectángulos de igual área.
- Elaboran estrategias para calcular áreas de triángulos rectángulos a partir del área de un rectángulo.
- Elaboran estrategias para calcular áreas de triángulos acutángulos, usando áreas de triángulos rectángulos.
- Calculan áreas de triángulos acutángulos, aplicando estrategias elaboradas.
- Elaboran estrategias para calcular áreas de triángulos obtusángulos a partir de paralelogramos.
- Explican la estrategia usada en la resolución de un problema relativo a cálculos de áreas de rectángulos.
- Evalúan la solución de problemas relativos a áreas en función del contexto del problema.
- Estiman áreas pedidas en un problema y cotejan esta estimación con la solución obtenida del problema.
Modifica o crea tu evaluación seleccionando las preguntas disponibles para este objetivo que te interesen. Solo debes hacer clic en el botón "Agregar pregunta".
Cada vez que sumes una pregunta, aumentará en una unidad el botón que flota al costado derecho de esta página. Si lo presionas verás el listado de preguntas de la evaluación que estás creando o modificando.
Si deseas buscar más preguntas por nivel, asignatura, eje, unidad, objetivo o un término, utiliza el buscador de Arma tu evaluación
Preguntas
Cubriendo un área rectangular
Enunciado
Alfonso quiere poner una alfombra en el piso de la sala donde ven televisión en su casa. La alfombra mide 2 m de ancho y 3 m de largo y el piso mide 3 m de ancho y 5 m de largo.
Al poner la algombra en la sala, ¿cuántos metros cuadrados del piso le quedarán sin estar cubiertos por ella?
Escribe todos los procedimientos de cálculo para responder.

Respuesta..........................................................................................
Respuesta
(área de la sala) - (área de la alfombra) = 15 m2 - 6 m2 = 9 m2
Respuesta: a Alfonso le quedarán sin cubrir 9 m2 del piso de la sala.
Construyendo estrategias para determinar el área de un rombo
Enunciado
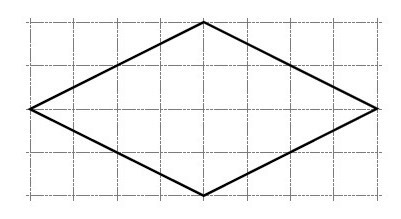
Observa el rombo en la cuadrícula, la que está formada por cuadraditos de 1 cm de longitud de lado. Explica o argumenta cómo obtienes el área del rombo.
 |
Respuesta......................................................................................................................................................
Respuesta
El eje de simetria vertical, divide en dos partes iguales el rombo, por lo tanto al doblar, se forma un cuadrado de lado 4 cm, cuya área es de 16 cm2
 |
Área del triángulo
Enunciado
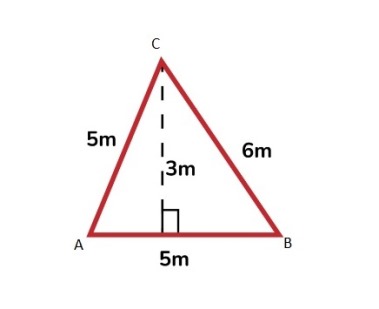
¿Cuál es el área del triángulo ABC?
 |
Alternativas
A) 16 m2
B) 15 m2
C) 12,5 m2
C) 7,5 m2
Respuesta
D) 7,5 m2
Área de triángulos
Enunciado
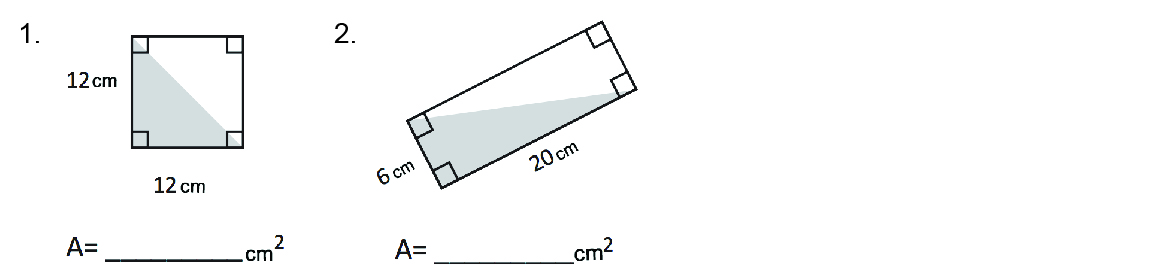
Calcula el área de los triángulos sombreados y explica el procedimiento que usaste.
Respuesta
1. El área sombreada es de 72 cm2.
2. El área sombreada es de 60 cm2.
Un procedimiento correcto para obtener la respuesta es calcular el área de los rectángulos y luego dividirla por 2.
Nota al profesor:
Para la explicación del procedimiento se espera que el estudiante sea capaz de redactar y dar a entender el método que usó, no es suficiente presentar una fórmula (para este caso asignar la mitad del puntaje), debe argumentar cómo y/o por qué lo hizo.
Nota para el profesor: Para evaluar la respuesta se puede utilizar la siguiente rúbrica
| Categoría | Descriptor |
|---|---|
| Destacado (todo el puntaje) |
Es estudiante es capaz de explicar de forma clara el método que usó, la explicación puede ir acompañada de una fórmula. Debe argumentar cómo y/o por qué utilizó ese método. |
| Logrado (mitad del puntaje) |
El estudiante no explica el procedimiento que ha utilizado y solo presenta una fórmula, o bien, presenta una explicación imprecisa o confusa. |
| Insuficiente (sin puntaje) |
El estudiante no presenta ninguna explicación. Si los resultados obtenidos son correctos, no asignar puntaje a la pregunta. |
Área de triángulos rectángulos
Enunciado
Calcula el área de los siguientes triángulos rectángulos:
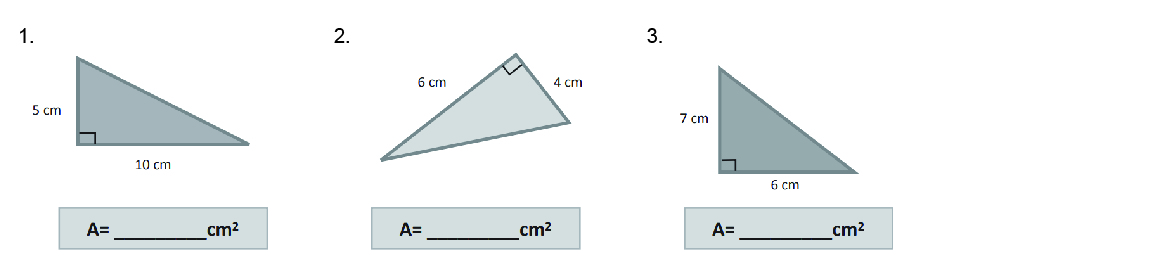
Respuesta
1. 25 cm2.
2. 12 cm2.
3. 21 cm2.
Área de un trapecio
Enunciado
Observa la siguiente figura:

¿Cuál es el área de la figura?
Alternativas
A) 22 cm2
B) 28 cm2
C) 38 cm2
D) 96 cm2
Respuesta
B) 28 cm2
Área de un triángulo obtusángulo
Enunciado
En la cuadrícula formada por cuadraditos de 1 cm por lado se dibujó un triángulo.
 |
¿Cuánto mide el área del triángulo dibujado?
_______________________________________________________________________________________________
Respuesta
El área del triángulo dibujado es 14 cm2
Calculando el área de un trapecio
Enunciado
¿Cuánto mide el área del siguiente trapecio?

Alternativas
A) 125 cm2
B) 200 cm2
C) 225 cm2
D) 250 cm2
Respuesta
C) 225 cm2
Calcular área de un trapecio
Enunciado
El trapecio ABCD está formado por tres triangulos equiláteros congruentes.

a) Calcula el área de uno de los triangulos.
Escribe los cálculos:

Respuesta...............................................
b) Calcula el área del trapecio.
Escribe los cálculos

Respuesta.............................................
Respuesta
a) (6 x7) : 2 = 21 cm2
b) 21 por 3 resulta 63 cm2; pues son tres triangulos iguales.
Calcular de área rombo
Enunciado
La cuadrícula está formada por cuadraditos de 1 cm por lado, en ella se dibujó un rombo.
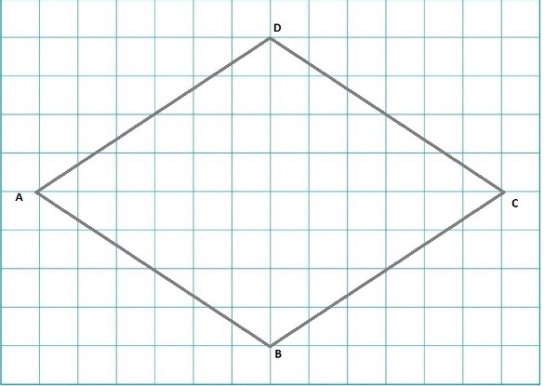 |
¿Cuál es el área del rombo?
Alternativas
A) 24 cm2
B) 48 cm2
C) 72 cm2
D) 96 cm2
Respuesta
B) 48 cm2
Cálculo de área de triángulos
Enunciado
Calcula el área de los siguientes triángulos:
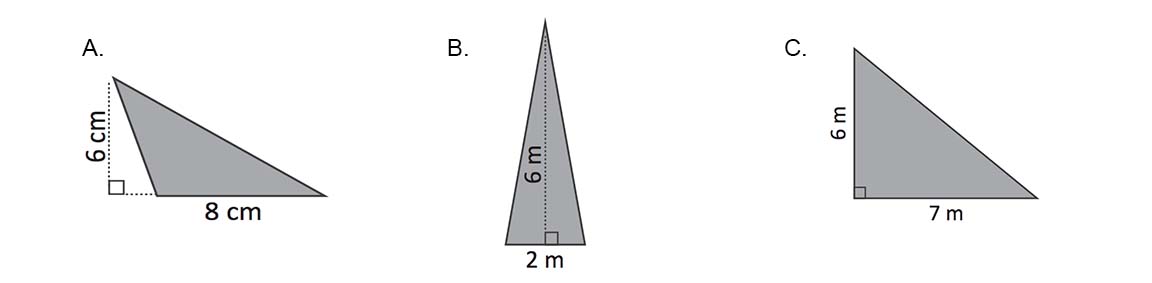
Respuesta
A. 24 cm2.
B. 6 m2.
C. 21 m2.
Cálculo de área de triángulos 2
Enunciado
Calcula el área de los siguientes triángulos:
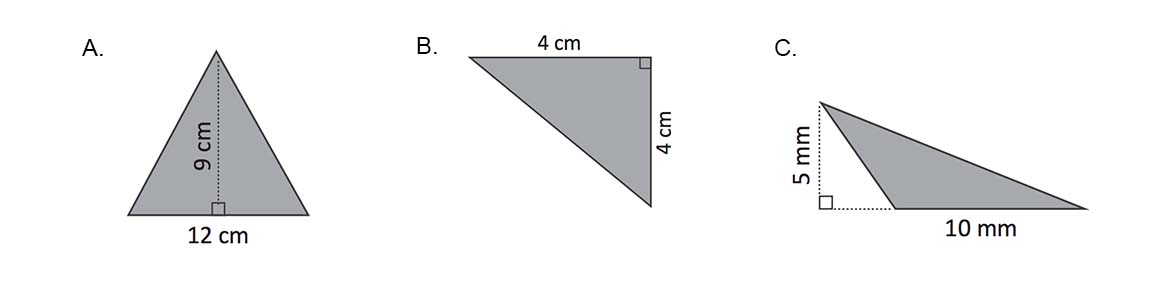
Respuesta
A. 54 cm2.
B. 8 cm2.
C. 25 mm2.
Cálculo de área de triángulos 3
Enunciado
Calcula el área de los siguientes triángulos:
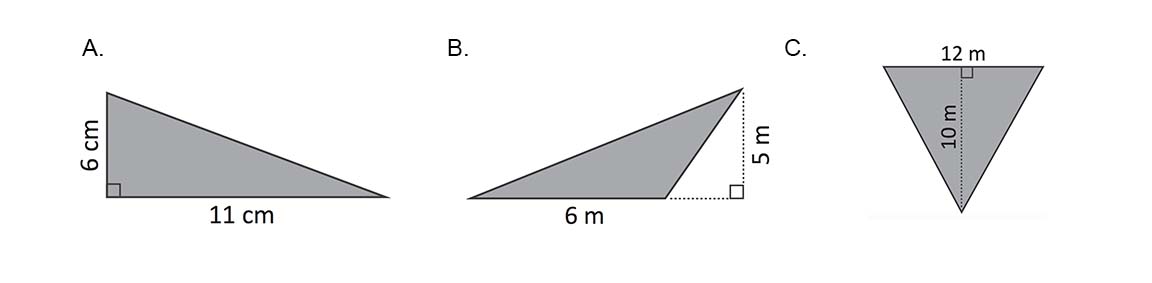
Respuesta
A. 33 cm2.
B. 15 m2.
C. 60 m2.
¿Cuál es el área del paralelogramo?
Enunciado
La figura muestra un paralelogramo sombreado dentro de un rectángulo.

¿Cuál es el área del paralelogramo?
| Escribe aquí tus cálculos y respuesta: |
Respuesta
24 cm2
Explicando cómo calcular áreas
Enunciado
Calcula el área de la siguiente figura.
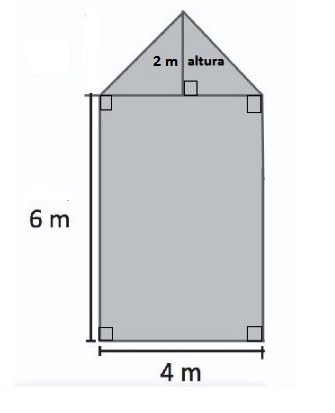
Escribe todos los procedimientos de cálculo.
 |
Respuesta .............................m2
Respuesta
El área de la figura es 28 m2.
Para evaluar la respuesta considerar los siguientes criterios:
| Categoría | Descripción |
|---|---|
| Destacado (todo el puntaje) |
El estudiante muestra todos los cálculos para calcular el área de l figura. El área del rectángulo 6x4=24 m2 Luego el área del triángulo $\frac{2x4}{2}$ = 4 m2 Suma ambos resultados 24 m2 + 4 m2 = 28 m2 |
| Logrado (mitad del puntaje) |
El estudiante muestra solo un cálculo en forma correcta: el área del rectángulo o el área del triángulo . O muestra el área de triangulo y rectángulo en forma correcta, pero no mustra la suma o total del área de la figura. |
| Insuficiente (sin puntaje) |
El estudiante no es capaz de calcular el área de la figura completa. |
Un problema de área 2
Enunciado
La cuadrícula está formada por cuadraditos de 1 cm por lado.
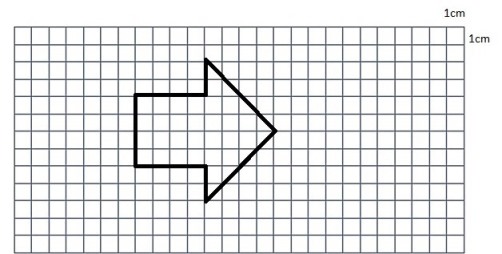 |
¿Cuál es el área de la figura dibujada en la cuadrícula?
El área de la figura es ...........................cm2.
Respuesta
Respuestas correctas:
a) usa el conteo de los cuadraditos, pintando o marcando en la figura y sumando las mitades de 4 cuadraditos de la punta de la flecha.
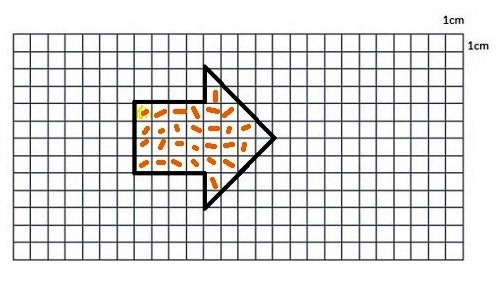 |
b) Descompone la figura formando dos cuadrados de 16 cm2, por lo tanto el área es de 32 cm2
 |
c) Calcula por partes. Aplica fórmula del área del cuadrado: 4 x 4 = 16 cm2 y del triángulo isósceles: (8 x 4 ) : 2 = 16 cm2 . Luego suma 16 + 16 = 32 cm2